题目内容
设直线L1:y1= k1x+b1 与 L2:y2= k2x+b2, 若L1⊥L2, 垂足为 H,则称直线L1 与 L2 是点 H的直角线.
(1)已知直线①y=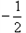 x+2;②y=x+ 2;③y=2x+2;④y=2x+4和点 C(0,2). 则直线_和_是点 C的直角线(序号即可);
x+2;②y=x+ 2;③y=2x+2;④y=2x+4和点 C(0,2). 则直线_和_是点 C的直角线(序号即可);
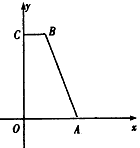
(2)如图,在平面直角坐标系中,直角梯形OABC的顶点A(3,0)、B(2,7)、C(0,7),P 为线段OC 上一点,:设过 B、P两点的直线为L1 ,过A、P两点的直线为 L2 ,若L1与 L2 是点 P的直角线,求直线L1与 L2 的解析式.
(1)已知直线①y=
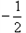 x+2;②y=x+ 2;③y=2x+2;④y=2x+4和点 C(0,2). 则直线_和_是点 C的直角线(序号即可);
x+2;②y=x+ 2;③y=2x+2;④y=2x+4和点 C(0,2). 则直线_和_是点 C的直角线(序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC的顶点A(3,0)、B(2,7)、C(0,7),P 为线段OC 上一点,:设过 B、P两点的直线为L1 ,过A、P两点的直线为 L2 ,若L1与 L2 是点 P的直角线,求直线L1与 L2 的解析式.
解.(1)画图象可知.直线①与直线③是点C的直角线;
(2)设 P坐标为 (0,m). 则 PA⊥PB于点.P. 因此,AB2=(3-2)2 + 72 = 50,
又∵PA2 - PO2+ OA2 = m2 + 32,PB2 = PC2+ BC2= (7-m)2 + 22,
∴.AB2 +PA2 + PB2=m2+52 + (7-m)2 +22 =50 解得:m1 = 1,m2 =6.
当 m =1 时,L1为:y1= 3x +1,L2 为:y2=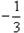 x+1
x+1
当 m= 6 时,L1为:y1=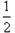 x+6,L2 为:y2= -2x+6.
x+6,L2 为:y2= -2x+6.
(2)设 P坐标为 (0,m). 则 PA⊥PB于点.P. 因此,AB2=(3-2)2 + 72 = 50,
又∵PA2 - PO2+ OA2 = m2 + 32,PB2 = PC2+ BC2= (7-m)2 + 22,
∴.AB2 +PA2 + PB2=m2+52 + (7-m)2 +22 =50 解得:m1 = 1,m2 =6.
当 m =1 时,L1为:y1= 3x +1,L2 为:y2=
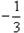 x+1
x+1当 m= 6 时,L1为:y1=
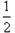 x+6,L2 为:y2= -2x+6.
x+6,L2 为:y2= -2x+6.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 设直线l1:y1=k1x+b1与l2:y2=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.
设直线l1:y1=k1x+b1与l2:y2=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.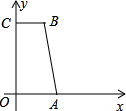 设直线l1:y1=k1x+b1与l2:y2=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.
设直线l1:y1=k1x+b1与l2:y2=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.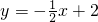 ;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2).则直线______ 和______是点C的直角线(填序号即可);
;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2).则直线______ 和______是点C的直角线(填序号即可);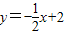 ;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2).则直线______ 和______是点C的直角线(填序号即可);
;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2).则直线______ 和______是点C的直角线(填序号即可);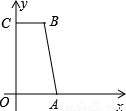
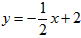 ;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2),则直线____和____是点C的直角线(填序号即可);
;②y=x+2;③y=2x+2;④y=2x+4和点C(0,2),则直线____和____是点C的直角线(填序号即可);