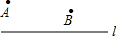题目内容
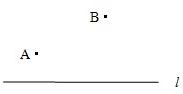22、如图，已知直线l和点A、B，在直线l上找一点P，使△PAB的周长最小，请说明理由．分析：由于△PAB的周长=PA+AB+PB，而AB是定值，故只需在直线l上找一点P，使PA+PB最小．如果设A关于l的对称点为A′，使PA+PB最小就是使PA′+PB最小．
解答：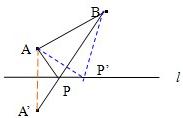
解：作法：
（1）作A关于l的对称点A′，
（2）连接A′B交l于点P．
则点P就是所要求作的点．
理由：在l上取不同于P的点P′，连接AP′、BP′．
∵A和A′关于直线l对称，
∴PA=PA′，P′A=P′A′，
而A′P+BP＜A′P′+BP′
∴PA+BP＜AP′+BP′
∴AB+AP+BP＜AB+AP′+BP′
即△ABP周长小于△ABP′周长．
解：作法：（1）作A关于l的对称点A′，
（2）连接A′B交l于点P．
则点P就是所要求作的点．
理由：在l上取不同于P的点P′，连接AP′、BP′．
∵A和A′关于直线l对称，
∴PA=PA′，P′A=P′A′，
而A′P+BP＜A′P′+BP′
∴PA+BP＜AP′+BP′
∴AB+AP+BP＜AB+AP′+BP′
即△ABP周长小于△ABP′周长．
点评：解这类问题的关键是把两条线段的和转化为一条线段，运用三角形三边关系解决．
练习册系列答案
相关题目
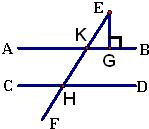28、如图，已知直线EF和AB，CD分别相交于点K，H，且EG⊥AB，∠CHF=60°，∠E=30°，试证明：AB∥CD．
如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE，∠COF=34°，则∠BOD的大小为（ ）
