题目内容
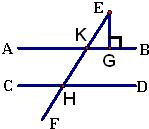 28、如图,已知直线EF和AB,CD分别相交于点K,H,且EG⊥AB,∠CHF=60°,∠E=30°,试证明:AB∥CD.
28、如图,已知直线EF和AB,CD分别相交于点K,H,且EG⊥AB,∠CHF=60°,∠E=30°,试证明:AB∥CD.分析:先由EG⊥AB,∠E=30°结合三角形内角和定理可求出∠EKG的度数,由对顶角相等可求出∠AKH的度数,再由∠CHF=60°即可求出∠AKH=∠CHF=60°,根据同位角相等,两直线平行,即可判断出AB∥CD.
解答:解:∵EG⊥AB,∠E=30°,
∴∠EKG=180°-∠EGK-∠E=180°-90°-30°=60°,
∴∠AKH=∠EKG=60°,
∵∠CHF=60°,
∴∠AKH=∠CHF=60°,
∴AB∥CD.
∴∠EKG=180°-∠EGK-∠E=180°-90°-30°=60°,
∴∠AKH=∠EKG=60°,
∵∠CHF=60°,
∴∠AKH=∠CHF=60°,
∴AB∥CD.
点评:本题涉及到三角形内角和定理、对顶角相等及平行线的判定定理,比较简单.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
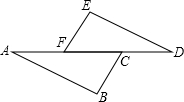 如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.
如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.
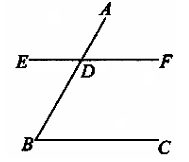
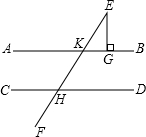 如图,已知直线EF和AB,CD分别相交于点K,H,且EG⊥AB,∠CHF=60°,∠E=30°,试证明:AB∥CD.
如图,已知直线EF和AB,CD分别相交于点K,H,且EG⊥AB,∠CHF=60°,∠E=30°,试证明:AB∥CD.