题目内容
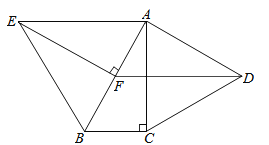
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
【答案】(1)证明见解析;(2)四边形EFDA是平行四边形.
【解析】
试题分析:(1)由△ABE是等边三角形可知:AE=BE,∠EAF=60°,于是可得到∠EFA=∠ACB,∠EAF=∠ABC,接下来依据AAS证明△ABC≌△EAF即可;
(2)由△ABC≌△EAF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD,然互再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.
试题解析:(1)证明:∵△ABE是等边三角形,EF⊥AB,∴∠EAF=60°,AE=BE,∠EFA=90°.
又∵∠ACB=90°,∠ABC=60°,∴∠EFA=∠ACB,∠EAF=∠ABC.
在△ABC和△EAF中,∵∠EFA=∠ACB,∠EAF=∠ABC,AE=BE,∴△ABC≌△EAF.
(2)结论:四边形EFDA是平行四边形.
理由:∵△ABC≌△EAF,∴EF=AC.∵△ACD是的等边三角形,∴AC=AD,∠CAD=60°,∴AD=EF.又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,∴∠BAD=∠BAC+∠CAD=90°,∴∠EFA=∠BAD=90°,∴EF∥AD.又∵EF=AD,∴四边形EFDA是平行四边形.

练习册系列答案
相关题目