题目内容
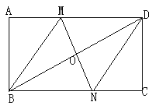
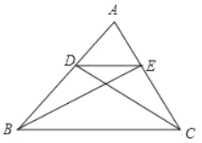
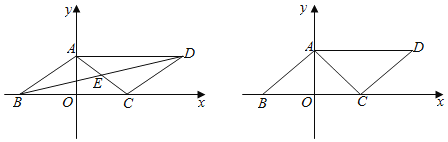
【题目】如图,已知□ABCD边BC在x轴上,顶点A在y轴上,对角线AC所在的直线为y=![]() +6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
+6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
(1)直接写出顶点D的坐标(______,______),对角线的交点E的坐标(______,______);
(2)求对角线BD的长;
(3)是否存在t,使S△POQ=![]() SABCD,若存在,请求出的t值;不存在说明理由.
SABCD,若存在,请求出的t值;不存在说明理由.
(4)在整个运动过程中,PQ的中点到原点O的最短距离是______cm,(直接写出答案)
【答案】(1)16;6;4;3;(2)BD=6![]() ;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为
;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为![]() .
.
【解析】
(1)令x=0,y=0代入解析式得出A,C坐标,进而利用平行四边形的性质解答即可;
(2)根据平行四边形的性质得出点B,D坐标,利用两点间距离解答即可;
(3)利用三角形的面积公式和平行四边形的面积公式列出方程解答即可;
(4)根据直角三角形斜边上中线等于斜边的一半可知,当PQ长度最短时,PQ的中点到原点O的距离最短解答即可.
(1)把x=0代入y=![]() +6,可得y=6,
+6,可得y=6,
即A的坐标为(0,6),
把y=0代入y=![]() +6,可得:x=8,
+6,可得:x=8,
即点C的坐标为(8,0),
根据平行四边形的性质可得:点B坐标为(-8,0),
所以AD=BC=16,
所以点D坐标为(16,6),
点E为对角线的交点,
故点E是AC的中点,
E的坐标为(4,3),
故答案为:16;6;4;3;
(2)因为B(-8,0)和D(16,6),
∴BD=![]() ;
;
(3)设时间为t,可得:OP=6-t,OQ=8-2t,
∵S△POQ= SABCD,
当0<t≤4时,![]() ,
,
解得:t1=2,t2=8(不合题意,舍去),
当4<t≤6时,![]() ,
,
△<0,不存在,
答:存在S△POQ=![]() SABCD,此时t值为2;
SABCD,此时t值为2;
(4)∵![]() ,
,
当t=![]() 时,PQ=
时,PQ=![]() ,
,
当PQ长度最短时,PQ的中点到原点O的距离最短,此时PQ的中点到原点O的最短距离为![]() PQ=
PQ=![]()
![]() =
=![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?