题目内容
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。

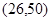
由题中规律可得出如下结论:设点Pm的横坐标的绝对值是n,
则在y轴右侧的点的下标分别是4(n-1)和4n-3,
在y轴左侧的点的下标是:4n-2和4n-1;
判断P100的坐标,就是看100=4(n-1)和100=4n-3和100=4n-2和100=4n-1这四个式子中哪一个有正整数解,从而判断出点的横坐标.
由上可得:点P第100次跳动至点P100的坐标是(26,50);
则在y轴右侧的点的下标分别是4(n-1)和4n-3,
在y轴左侧的点的下标是:4n-2和4n-1;
判断P100的坐标,就是看100=4(n-1)和100=4n-3和100=4n-2和100=4n-1这四个式子中哪一个有正整数解,从而判断出点的横坐标.
由上可得:点P第100次跳动至点P100的坐标是(26,50);

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
