Question

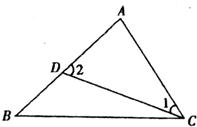26、如图，△ABC中，点D在AB上，请填上一个你认为适合的条件

∠1=∠B或∠2=∠ACB或AD：AC=AC：AB或AC²=AD•AB

，使得△ACD∽△ABC．

Answer 1

分析：要使△ACD∽△ABC，已知有一对公共角，则只要添加另一对角相等或该角的两边对应成比例即可．

解答：解：∵∠A=∠A
∴当∠1=∠B或∠2=∠ACB或AD：AC=AC：AB或AC²=AD•AB时，△ACD∽△ABC．

点评：此题考查了相似三角形的判定，
①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；
②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；
③如果两个三角形的两个对应角相等，那么这两个三角形相似．平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．