题目内容
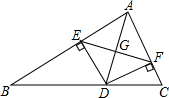 如图,△ABC中,若AD平分∠BAC,过D点作DE⊥AB,DF⊥AC,分别交AB、AC于E、F两点.求证:AD⊥EF.
如图,△ABC中,若AD平分∠BAC,过D点作DE⊥AB,DF⊥AC,分别交AB、AC于E、F两点.求证:AD⊥EF.分析:根据角平分线得出DE=DF,∠EAD=∠FAD,∠AED=∠AFD=90°,推出∠EDA=∠FDA,根据等腰三角形性质推出即可.
解答:证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠EAD=∠FAD,∠AED=∠AFD=90°,
∵∠AED+∠EAD+∠EDA=180°,∠FAD+∠AFD+∠ADF=180°,
∴∠EDA=∠FDA,
∵DE=DF,
∴AD⊥EF三线合一).
∴DE=DF,∠EAD=∠FAD,∠AED=∠AFD=90°,
∵∠AED+∠EAD+∠EDA=180°,∠FAD+∠AFD+∠ADF=180°,
∴∠EDA=∠FDA,
∵DE=DF,
∴AD⊥EF三线合一).
点评:本题考查了角平分线性质,三角形的内角和定理,等腰三角形的性质的应用,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
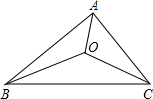 如图,△ABC中,若∠A=80°,O为三条角平分线的交点,则∠BOC=
如图,△ABC中,若∠A=80°,O为三条角平分线的交点,则∠BOC= 10、下列说法,正确的有( )个
10、下列说法,正确的有( )个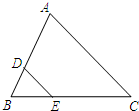 如图,△ABC中,若DE∥AC,
如图,△ABC中,若DE∥AC,