题目内容

如图所示，二次函数y=ax²+bx+c的图象与x轴负半轴相交于A、B两点，Q（n， $数学公式$ ）是二次函数y=ax²+bx+c图象上一点，且AQ⊥BQ，则a的值为

A.
- $数学公式$
B.
- $数学公式$
C.
-1
D.
-2

D
分析：由勾股定理，及根与系数的关系可得．
解答：设ax²+bx+c=0的两根分别为x₁与x₂，
依题意有（x₁-n）²+ $\text{[math]}$ +（x₂-n）²+ $\text{[math]}$ =（x₁-x₂）²，
化简得：n²-n（x₁+x₂）+ $\text{[math]}$ +x₁x₂=0．
有n²+ $\text{[math]}$ n+ $\text{[math]}$ + $\text{[math]}$ =0，
∴an²+bn+c=- $\text{[math]}$ a．
∵（n， $\text{[math]}$ ）是图象上的一点，
∴an²+bn+c= $\text{[math]}$ ，
∴- $\text{[math]}$ a= $\text{[math]}$ ，
∴a=-2．
故选D．
点评：本题是一道二次函数的综合试题，考查了二次函数的性质和图象，解题的关键是注意数形结合思想．

练习册系列答案

孟建平系列一课三练课时导学系列答案

激活课堂课时作业系列答案

优等生题库系列答案

亮点激活教材多元演练系列答案

小助手高效课时学案系列答案

金质课堂系列答案

初中同步学习导与练导学探究案系列答案

金版课堂系列答案

53天天练系列答案

新黄冈兵法同步考试兵法系列答案

相关题目

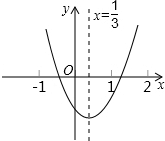小明从如图所示的二次函数y=ax²+bx+c的图象中，观察得出了下面六条信息：
①c＜0；②abc＞0；③a-b+c＞0；④2a-3b=0；⑤4a+2b+c＞0；⑥一元二次方程ax²+bx+c=0有两异号实根．
你认为其中正确信息的个数有（　　）

一男生在校运会的比赛中推铅球，铅球的行进高度y（m）与水平距离x（m）之间的关系用如图所示的二次函数图象表示．（

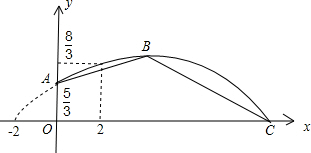铅球从A点被推出，实线部分表示铅球所经过的路线）
（1）由已知图象上的三点，求y与x之间的函数关系式；
（2）求出铅球被推出的距离；
（3）若铅球到达的最大高度的位置为点B，落地点为C，求四边形OABC的面积．

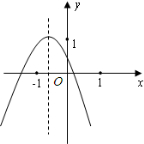如图所示的二次函数y=ax²+bx+c的图象中，刘星同学观察得出了下面四条信息：
（1）b²-4ac＞0；（2）c＞1；（3）2a-b＜0；（4）a+b+c＜0．你认为其中错误的有（　　）

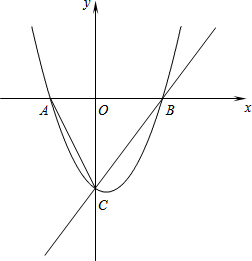如图所示，二次函数 y=ax²+bx+c的图象与x轴交于点A和点B（A、B分别位于原点O的两侧），与y轴的下半轴交于点C，且tan∠OAC=2，AB=CB=5．
（1）求直线BC和二次函数的解析式；
（2）直线BC上是否存在这样的点P，使△PAB和△OBC相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．

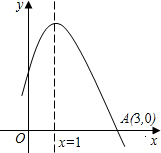（2012•甘谷县模拟）如图所示是二次函数y=ax²+bx+c图象的一部分，图象过A点（3，0），对称轴为x=1，给出四个结论：①b²-4ac＞0；②2a+b=0；③a+b+c=0；④当x=-1或x=3时，函数y的值都等于0．把正确结论的序号填在横线上