题目内容
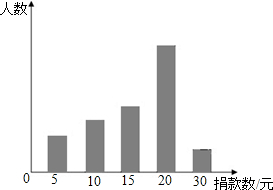
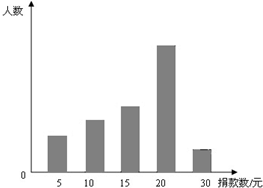 21、某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
21、某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.(1)他们一共抽查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1500名学生,请估算全校学生共捐款多少元?
分析:(1)根据捐15元和20元得人数共39人及这两组所占的总人数比例可求出总人数,;
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;
(3)求出这组数据的平均数,再估算.
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;
(3)求出这组数据的平均数,再估算.
解答:解:(1)设捐15元的人数为5x,则根据题意捐20元的人数为8x.
∴5x+8x=39,
∴x=3,
∴一共调查了3x+4x+5x+8x+2x=66(人).
(2)5个组的人数分别为9,12,15,24,6.
所以这组数据的众数是20(元),中位数是15(元).
(3)全校学生共捐款:(9×5+12×10+15×15+24×20+6×30)÷66×1500=23864(元).
∴5x+8x=39,
∴x=3,
∴一共调查了3x+4x+5x+8x+2x=66(人).
(2)5个组的人数分别为9,12,15,24,6.
所以这组数据的众数是20(元),中位数是15(元).
(3)全校学生共捐款:(9×5+12×10+15×15+24×20+6×30)÷66×1500=23864(元).
点评:本题考查的是条形统计图的运用,读懂统计图,掌握众数、中位数的性质是关键.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目