题目内容
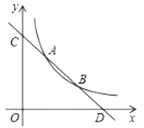
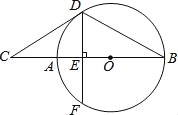
【题目】如图,AB是圆O的直径,点C在BA的延长线上,直线CD与圆O相切于点D,弦DF⊥AB于点E,连接BD,CD=BD=4![]() ,则OE的长度为( )
,则OE的长度为( )
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
【答案】B
【解析】
连结OD,根据切线的性质得∠ODC=90°,根据等腰三角形的性质得出∠B=∠C=∠ODB,于是可根据三角形外角性质得∠DOE=2∠B=2∠C,进而求得∠DOE=60°,解直角三角形即可求得OE.
解:连结OD,如图,
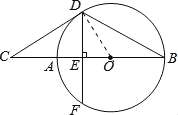
∵直线CD与⊙O相切于点D,
∴OD⊥CD,
∴∠ODC=90°,
∵CD=BD,
∴∠C=∠B,
∵OD=OB,
∴∠B=∠ODB,
∴∠DOE=∠B+∠ODB=2∠B,
∴∠DOE=2∠C,
在Rt△OCD中,∠DOE=2∠C,则∠DOE=60°,∠C=30°,
∵CD=4![]() ,
,
∴OD=![]() ×4
×4![]() =4,
=4,
∵DF⊥AB,∠DOE=60°,
∴OE=![]() ×4=2,
×4=2,
故选:B.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | ﹣1 | 0 | m | 8 | … |
(1)m的值为 ;
(2)抛物线y=ax2+bx+c的对称轴为 ;
(3)这个二次函数的解析式为 ;
(4)当0<x<3时,则y的取值范围为 .