Question

【题目】如图1，在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A、B分别在轴和轴上，已知OA=5，OB=3，点D的坐标是（0，1），点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动，当点P与点A重合时，运动停止，设运动的时间为秒．

（1）点P运动到与点C重合时，求直线DP的函数解析式；

（2）求△OPD的面积S关于的函数解析式，并写出对应的取值范围；

（3）点P在运动过程中，是否存在某些位置使△ADP是不以DP为底边的等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2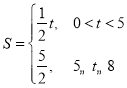）；（3）存在满足条件的点P，其坐标为或或

【解析】

（1）先求出C点坐标，然后用待定系数法求直线DP的解析式即可；

（2）分点P在线段BC上和在线段AC上两种情况，分别求得s关于的函数解析式；

（3）当点P在线段BC上时，可用t表示出点P点坐标，再分别表示出DP、AP和AD的长，然后再分DP=AP、DP=AD和AP=AD三种情况分别求得关于t的方程，即可求得P点的坐标；当点P在线段AC上时，则只能有PD=AD，则点D在线段AP的垂直平分线上，即可确定线段AP中点的坐标，从而可求得P点坐标．

解：（1），，且四边形为长方形，

，

∴当点P与点C重合时，P点坐标为，

设直线DP解析式为，

，解得，

直线DP解析式为．

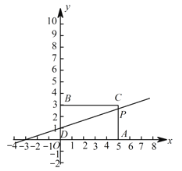
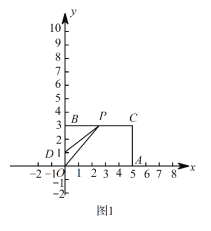
（2）当时，如图1，

则，且，

，

当时，，

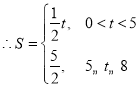．存在满足条件的点P，其坐标为或或

（3）存在，理由如下：

当点P在线段BC上时，如图2，

设P点坐标为，

，，

，，，

∵△ADP是不以DP为底边的等腰三角形

∴有，两种情况，

①当时，则有，解得，此时P点坐标为；

②当时，则有，解得（舍去）或，此时P点坐标为；

当点P在线段AC上时，

，

∴只有，

在线段的垂直平分线上，

∴线段的中点坐标为，

∴P点坐标为；

综上可知存在满足条件的点P，其坐标为或或．