题目内容
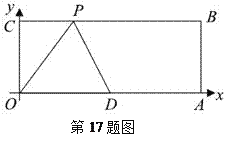
【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动![]() 秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(1)OE= ,OF= (用含t的代数式表示)
(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.

【答案】(1)6-t,![]() +t;(2)①直线DE的解析式为:y=-
+t;(2)①直线DE的解析式为:y=-![]() ;②
;②
【解析】
(1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据E点与F点的运动速度与运动时间即可用含t的代数式表示OE,OF;
(2)①由翻折的性质可知:△OPF≌△DPF,进而可得:DF=OF,然后由t=1时,DF=OF=![]() ,CF=OC-OF=
,CF=OC-OF=![]() ,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
②先确定出k的值,再分情况计算S的表达式,并确认b的取值.
(1)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点E从点A出发以相等的速度沿AO向终点O运动,
秒时,动点E从点A出发以相等的速度沿AO向终点O运动,
∴当点E的运动时间为t(秒)时,
AE=t,OF=![]() +t,
+t,
则OE=OA-AE=6-t,
故答案为:6-t,![]() +t;
+t;
(2)①当t=1时,OF=1+![]() =
=![]() ,OE=6-1=5,则CF=OC-OF=3-
,OE=6-1=5,则CF=OC-OF=3-![]() =
=![]() ,
,

由折叠可知:△OEF≌△DEF,
∴OF=DF=![]() ,
,
由勾股定理,得:CD=1,
∴D(1,3);
∵E(5,0),
∴设直线DE的解析式为:y=mx+n(k≠0),
把D(1,3)和E(5,0)代入得:![]() ,解得:
,解得: ,
,
∴直线DE的解析式为:y=-![]() ;
;
②∵MN∥DE,
∴MN的解析式为:y=-![]() ,
,
当y=3时,-![]() =3,x=
=3,x=![]() (b-3)=
(b-3)=![]() b-4,
b-4,
∴CM=![]() b-4,
b-4,
分三种情况:
i)当M在边CB上时,如图2,

∴BM=6-CM=6-(![]() b-4)=10-
b-4)=10-![]() b,
b,
DM=CM-1=![]() b-5,
b-5,
∵0≤DM<5,即0≤![]() b-5<5,
b-5<5,
∴![]() ≤b<
≤b<![]() ,
,
∴S=![]() BMAB=
BMAB=![]() ×3(10
×3(10![]() b)=15-2b=-2b+15(
b)=15-2b=-2b+15(![]() ≤b<
≤b<![]() );
);
ii)当M与点B重合时,b=![]() ,S=0;
,S=0;
iii)当M在DB的延长线上时,如图3,

∴BM=CM-6=![]() b-10,
b-10,
DM=CM-1=![]() b-5,
b-5,
∵DM>5,即![]() b-5>5,
b-5>5,
∴b>![]() ,
,
∴S=![]() ×3(
×3(![]() b10)=2b-15(b>
b10)=2b-15(b>![]() );
);
综上, .
.

 名校课堂系列答案
名校课堂系列答案