题目内容
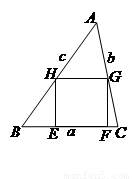
 如图,通过△ABC内部一点Q引平行于三角形三边的直线,这些直线分三角形为六个部分,已知三个平行四边形部分的面积为S1,S2,S3,求△ABC的面积.
如图,通过△ABC内部一点Q引平行于三角形三边的直线,这些直线分三角形为六个部分,已知三个平行四边形部分的面积为S1,S2,S3,求△ABC的面积.
 =S△QCE=
=S△QCE= =
= =
= ,
,所以S′2S′3=
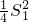 ①
①同理可得S′1S′2=
 ,②
,②S′3S′1=
 ,③
,③从①,②,③中可以解得
S′1=
 ,S′2=
,S′2= ,S′3=
,S′3= .
.所以S△ABC=S1+S2+S3=
 +
+ +
+ .
.答:△ABC的面积是
 +
+ +
+ .
.分析:设S△QDG=S′1,S△QIE=S′2,S△QFH=S′3,则所以S′2S′3=
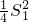 ①,同理可得S′1S′2=
①,同理可得S′1S′2= ,②S′3S′1=
,②S′3S′1= ,③
,③从①,②,③中可以解得△ABC的面积.
点评:此题主要考查学生对相似三角形的判定与性质和三角形面积的理解和掌握,此题的关键是求出①、②、③式,从中可以解得△ABC的面积.

问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
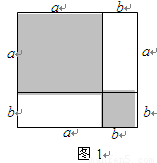
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
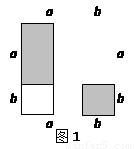
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用
1.已知:多项式M =2a2-a+1 ,N =a2-2a .试比较M与N的大小.
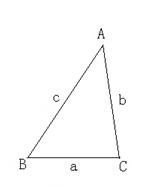
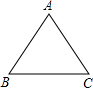
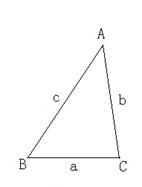
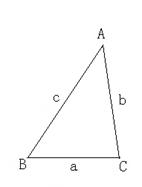
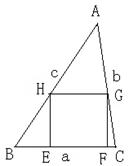
2.已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
拓展延伸
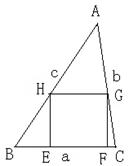
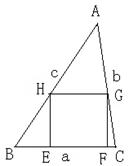
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?
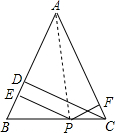 【老题重现】
【老题重现】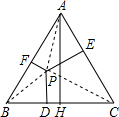


 ,
, .
.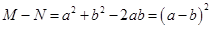 .
.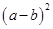 >0.
>0.