题目内容
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.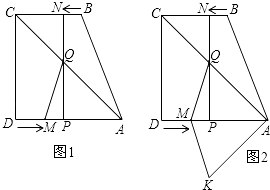
(1)AM= , AP= . (用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC等于.
【答案】
(1)8﹣2t;2+t
(2)
解:∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),解得t=2
(3)
解:①存在时刻t=1,使四边形AQMK为菱形.理由如下:
∵NP⊥AD,QP=PK,
∴当PM=PA时有四边形AQMK为菱形,
∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°,
∴∠CAD=45°.
∴四边形AQMK为正方形,则CD=AD,
∵AD=8,
∴CD=8,
∴AC=8 ![]() .
.
【解析】解:(1)如图1.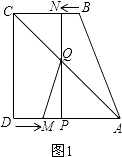
∵DM=2t,
∴AM=AD﹣DM=8﹣2t.
∵在直角梯形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P,
∴四边形CNPD为矩形,
∴DP=CN=BC﹣BN=6﹣t,
∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(1)由DM=2t,根据AM=AD﹣DM即可求出AM=8﹣2t;先证明四边形CNPD为矩形,得出DP=CN=6﹣t,则AP=AD﹣DP=2+t;(2)根据四边形ANCP为平行四边形时,可得6﹣t=8﹣(6﹣t),解方程即可;(3)①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6﹣t﹣2t=8﹣(6﹣t),求解即可,②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.

 天天练口算系列答案
天天练口算系列答案【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒