题目内容
(2002•徐州)如图,在矩形ABCD中,AB=4,BC=3,将矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,AB与x轴正方向成30°的角,求点B、C的坐标.
【答案】分析:矩形在直角坐标系中,分别过点B、C作x轴的垂线,垂足分别为E、F,过点B作BG⊥CF于G,矩形的长宽知道,AB与x轴正方向成30°的角,设AB与CF交于点H,然后在直角三角形中解出OF,FC.
解答: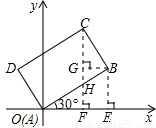 解:分别过点B、C作x轴的垂线,垂足分别为E、F,过点B作BG⊥CF于G,
解:分别过点B、C作x轴的垂线,垂足分别为E、F,过点B作BG⊥CF于G,
在Rt△OEB中,OE=AB•cos 30°=4x =2
=2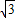 ,EB=4sin30°=2,
,EB=4sin30°=2,
所以B(2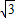 ,2).
,2).
设AB与CF交于点H,
因为∠AHF=∠CHB,
所以∠BCG=∠BAE=30°.
Rt△BGC中,BG=BC•sin30°=3x =
= ,CG=BC•cos30°=
,CG=BC•cos30°=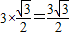 ,
,
所以OF=OE-EF=OE-BG=2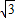 -
- ,FC=FG=EB+GC=2+
,FC=FG=EB+GC=2+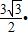
∴C(2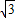 -
- ,2+
,2+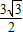 ).
).
点评:本题主要考查矩形的性质,掌握直角三角形的性质很重要.虽然题不是很难但要细心.
解答:
 解:分别过点B、C作x轴的垂线,垂足分别为E、F,过点B作BG⊥CF于G,
解:分别过点B、C作x轴的垂线,垂足分别为E、F,过点B作BG⊥CF于G,在Rt△OEB中,OE=AB•cos 30°=4x
 =2
=2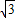 ,EB=4sin30°=2,
,EB=4sin30°=2,所以B(2
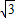 ,2).
,2).设AB与CF交于点H,
因为∠AHF=∠CHB,
所以∠BCG=∠BAE=30°.
Rt△BGC中,BG=BC•sin30°=3x
 =
= ,CG=BC•cos30°=
,CG=BC•cos30°=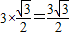 ,
,所以OF=OE-EF=OE-BG=2
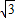 -
- ,FC=FG=EB+GC=2+
,FC=FG=EB+GC=2+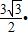
∴C(2
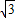 -
- ,2+
,2+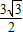 ).
).点评:本题主要考查矩形的性质,掌握直角三角形的性质很重要.虽然题不是很难但要细心.

练习册系列答案
相关题目



 于点Q,连接OQ.当点P沿x轴的正方向运动时,Rt△QOP的面积( )
于点Q,连接OQ.当点P沿x轴的正方向运动时,Rt△QOP的面积( )