题目内容
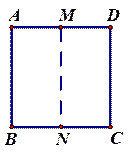
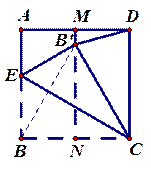
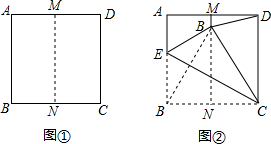 把正方形ABCD对折,得到折痕MN(如图①),展开后把正方形ABCD沿CE折叠,使点B落在MN上的点B′处,连接B′D(如图②).试求∠BCB′及∠ADB′的度数.
把正方形ABCD对折,得到折痕MN(如图①),展开后把正方形ABCD沿CE折叠,使点B落在MN上的点B′处,连接B′D(如图②).试求∠BCB′及∠ADB′的度数.分析:利用翻折变换的性质得出以及垂直平分线的性质得出BC=B′C,BB′=B′C,进而得出△B′BC是等边三角形,再利用等腰三角形的性质求出∠ADB′的度数即可.
解答: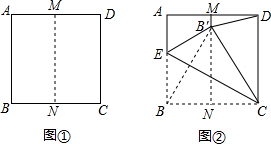 解:∵点B落在MN上的点B′处,把正方形ABCD对折,得到折痕MN,
解:∵点B落在MN上的点B′处,把正方形ABCD对折,得到折痕MN,
∴BC=B′C,BB′=B′C,
∴BC=BB′=B′C,
∴△B′BC是等边三角形,
∴∠BCB′=60°,
∴∠B′CD=30°,
∵DC=B′C,
∴∠CB′D=∠CDB′,
∴∠CB′D=∠CDB′=
×150°=75°,
∴∠ADB′=15°.
 解:∵点B落在MN上的点B′处,把正方形ABCD对折,得到折痕MN,
解:∵点B落在MN上的点B′处,把正方形ABCD对折,得到折痕MN,∴BC=B′C,BB′=B′C,
∴BC=BB′=B′C,
∴△B′BC是等边三角形,
∴∠BCB′=60°,
∴∠B′CD=30°,
∵DC=B′C,
∴∠CB′D=∠CDB′,
∴∠CB′D=∠CDB′=
| 1 |
| 2 |
∴∠ADB′=15°.
点评:此题主要考查了翻折变换的性质以及等腰直角三角形的性质,根据已知得出DC=B′C进而得出∠CB′D=∠CDB′是解题关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
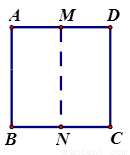
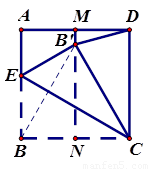
 15、如图,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折到MN上的同一点,折痕为BF,请回答下列问题:
15、如图,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折到MN上的同一点,折痕为BF,请回答下列问题: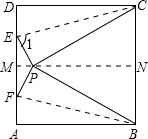 如图,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折到MN上的同一点,折痕为BF,则∠CPB的度数是
如图,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折到MN上的同一点,折痕为BF,则∠CPB的度数是