Question

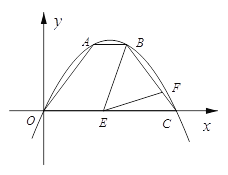
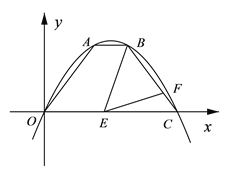
【题目】如图，一条抛物线经过原点和点C（8，0），A、B是该抛物线上的两点，AB∥x轴，点A坐标为（3，4），点E在线段OC上，点F在线段BC上，且满足∠BEF=∠AOC.

（1）求抛物线的解析式；

（2）若四边形OABE的面积为14，求S△ECF；

（3）是否存在点E，使得△BEF为等腰三角形？若存在，求点E的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）；（3）存在点E，点E的坐标为(2，0)或(3，0) 或(，0)

【解析】试题分析：（1）根据题意可设该抛物线的解析式为：y=ax（x-8）（a≠0）．然后将点A的坐标代入求值即可；

（2）先求出由相似三角形△AOE∽△ECF，求得面积比等于相似比的平方，则易求△ECF的面积；

（3）需要分类讨论：当AE=EF、AF=EF和AE=AF时，分别求得点E的坐标．

试题解析：

（1）设抛物线解析式为，

把A（3，4）代入得：

∴

∴抛物线解析式为，即

（2）∵AB∥x轴

∴四边形OABC关于抛物线对称轴对称

∴∠AOC=∠BCO，∴B（5，4）

∴AB=2，BC=OA=5

∵四边形OABE的面积为14

∴OE=5

∴CE=3，BE=4

∴

∵∠BEF=∠AOC=∠BCO, ∠EBF=∠CBE

∴△BEF∽△BCE

∴

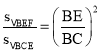
即

∴

(3)存在点E使得△BEF为等腰三角形

当BE=BF时，则∠BEF=∠BFE

∵∠BEF=∠ACO=∠BCO

∴∠BFE=∠BCE

∴EF与EC重合

∴∠BEC=∠BEF=∠AOC

∴OA∥BE

∵AB∥x轴

∴OE=AB=2

∴E(2，0)

当EB=EF时,则∠EBF=∠EFB

∵△BEF∽△BCE

∴∠BEC=∠BFE

∴∠BEC=∠EBF

∴EC=BC=5

∴OE=OC-EC=8-5=3

∴E(3，0)

当FB=FE时，则∠FBE=∠FEB

∴∠BCO=∠FEB=∠FBE

∴BE=EC，即点E在BC的中垂线上

过E作EM⊥BC，垂足为M；过A作AN⊥OC，垂足为N，

则CM= ,ON=3，OA=5

∵∠AON=∠ECM，∠ANO=∠

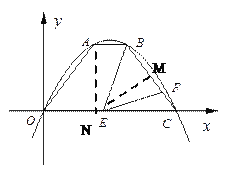
∴△AON∽△ECM

∴ 即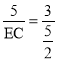

∴EC=

∴OE=OC-EC=

∴E(，0)

∴综上所述，存在点E，点E的坐标为(2，0)或(3，0) 或(，0)