题目内容
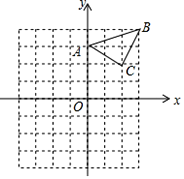
【题目】如图是单位长度为1的正方形网格，若A，B两点的坐标分别为
，
.
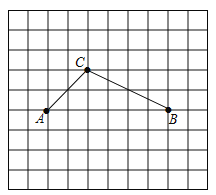
请解决下列问题：
（1）在网格图中画出平面直角坐标系，并直接写出点C的坐标_________.
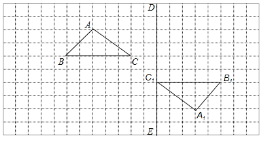
（2）将图中三角形ABC沿x轴向右平移1个单位，再沿y轴向上平移2个单位后得到三角形
，则
的坐标为_________；
的坐标为_________；
的坐标为_________；
（3）在y轴上是否存在点P，使得三角形
的面积为4，若存在，请直接写出P点坐标：若不存在，请说明理由.
【答案】（1）图略， 
；（2）
，
，
；（3）存在，
.
【解析】
（1）利用A、B点的坐标建立平面直角坐标系，然后写出点C的坐标；
（2）利用点平移的坐标变换规律分别写出点A1、B1、C1的坐标，然后描点即可；
（3）设P（0，t），根据三角形面积公式得到
2×|t﹣6|=4，然后解绝对值方程求出t，从而得到P点坐标．
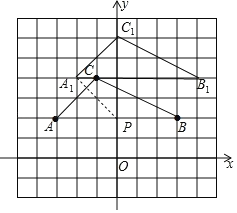
（1）如图，C点坐标为（﹣1，4）；
（2）如图，△A1B1C1为所作；A1的坐标为（﹣2，4）；B1的坐标为（4，4）；C1的坐标为（0，6）．
故答案为：（﹣1，4），（﹣2，4），（4，4），（0，6）；
（3）存在．
设P（0，t），根据题意得：2×|t﹣6|=4，解得：t=2或t=10，所以满足条件的P点坐标为（0，2）或（0，10）．
练习册系列答案
相关题目
