题目内容
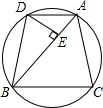 如图,已知圆内接△ABC中,AB>AC,D为
如图,已知圆内接△ABC中,AB>AC,D为 | BAC |
分析:在BA上截取BF=CA,连DF,DC,由D为
的中点,根据在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等得到DB=DC,易得△DBF≌△DCA,得到AE=EF,于是有BF=BE-EF=BE-AE=CA,因此BD2-AD2=BE2-AE2=(BE+AE)(BE-AE)=AB•AC.
 |
| BAC |
解答: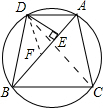 证明:在BA上截取BF=CA,连DF,DC,如图,
证明:在BA上截取BF=CA,连DF,DC,如图,
∵D为
的中点,
∴DB=DC,
又∵∠DBF=∠ACD,
∴△DBF≌△DCA,
∴DF=DA,
而DE⊥AB,
∴AE=EF,
∴BF=BE-EF=BE-AE=CA,
又∵BD2=BE2+DE2,AD2=AE2+DE2,
∴BD2-AD2=BE2-AE2=(BE+AE)(BE-AE)=AB•AC,即证.
 证明:在BA上截取BF=CA,连DF,DC,如图,
证明:在BA上截取BF=CA,连DF,DC,如图,∵D为
 |
| BAC |
∴DB=DC,
又∵∠DBF=∠ACD,
∴△DBF≌△DCA,
∴DF=DA,
而DE⊥AB,
∴AE=EF,
∴BF=BE-EF=BE-AE=CA,
又∵BD2=BE2+DE2,AD2=AE2+DE2,
∴BD2-AD2=BE2-AE2=(BE+AE)(BE-AE)=AB•AC,即证.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了三角形全等的判定与性质和等腰三角形的性质以及勾股定理.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
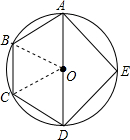 如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是
如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是 BCM=∠DCN.
BCM=∠DCN.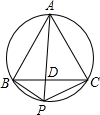 如图,已知圆内接等边△ABC,在劣弧BC上有一点P.若AP与BC交于点D,且PB=21,PC=28,则PD=
如图,已知圆内接等边△ABC,在劣弧BC上有一点P.若AP与BC交于点D,且PB=21,PC=28,则PD=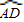 的中点,则△ADE的面积是 .
的中点,则△ADE的面积是 .