题目内容
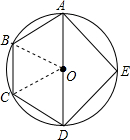 如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是
如图,已知圆内接四边形ABCD中,对角线AD是⊙O的直径,AB=BC=CD=2,E是 | AD |
分析:四边形ABCD是梯形,连接OB,则OBCD是菱形,即可求得AD的长,而△AED是等腰直角三角形,就可求得△ADE的面积.
解答: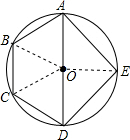 解:连接EO,
解:连接EO,
∵AB=BC=CD=2,
∴∠AOB=180÷3=60°,
∴△AOB是等边三角形,
那么OA=AB=2,那么AD=2OA=4.
∵E是
的中点,
∴AE=DE,
∴EO⊥AD,
∵EO=2,
∴△ADE的面积=
×4×2=4.
 解:连接EO,
解:连接EO,∵AB=BC=CD=2,
∴∠AOB=180÷3=60°,
∴△AOB是等边三角形,
那么OA=AB=2,那么AD=2OA=4.
∵E是
 |
| AD |
∴AE=DE,
∴EO⊥AD,
∵EO=2,
∴△ADE的面积=
| 1 |
| 2 |
点评:本题用到的知识点为:弦相等,那么所对的圆心角也相等.

练习册系列答案
相关题目
 BCM=∠DCN.
BCM=∠DCN. BCM=∠DCN.
BCM=∠DCN.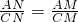 .
.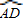 的中点,则△ADE的面积是 .
的中点,则△ADE的面积是 .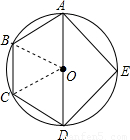
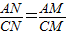 .
.