题目内容
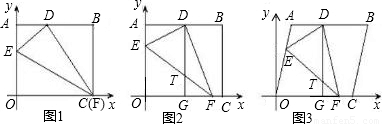
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在x轴和y轴上在OA、OC边上选取适当的点E、F,连接EF,将△EOF沿EF折叠,使点O落在AB边上的点D处。
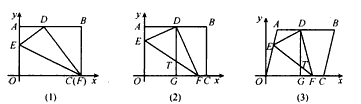
(1)如图(1),当点F与点C重合时,OE的长度为____;
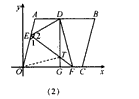
(2)如图(2),当点F与点C不重合时,过点D作DG∥y轴交EF于点T,交OC于点G。
求证:EO=DT;
(3)在(2)的条件下,设T(x,y),写出y与x之间的函数关系式:____,自变量x的取值范围是____;
(4)如图(3),将矩形OABC变为平行四边形,放在平面直角坐标系中,且OC=10,OC边上的高等于8,点F与点C不重合,过点D作DG∥y轴交EF 于点T,交OC于点G,求出这时T(x,y)的坐标y与x之间的函数关系式 (不求自变量x的取值范围)。
(2)如图(2),当点F与点C不重合时,过点D作DG∥y轴交EF于点T,交OC于点G。
求证:EO=DT;
(3)在(2)的条件下,设T(x,y),写出y与x之间的函数关系式:____,自变量x的取值范围是____;
(4)如图(3),将矩形OABC变为平行四边形,放在平面直角坐标系中,且OC=10,OC边上的高等于8,点F与点C不重合,过点D作DG∥y轴交EF 于点T,交OC于点G,求出这时T(x,y)的坐标y与x之间的函数关系式 (不求自变量x的取值范围)。
| 解:(1)5 | |
| (2)∵△EDF是由△EFO折叠得到的, ∴∠1=∠2, 又DC∥y轴, ∴∠l=∠3, ∴∠2=∠3, ∴DE=DT, ∵DE= EO, ∴ EO=DT; |
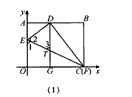 |
(3)y=-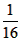 x2+4.4,4<x≤8. x2+4.4,4<x≤8. |
|
|
(4)连接OT, |
 |

练习册系列答案
相关题目
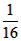 x2+4。
x2+4。 
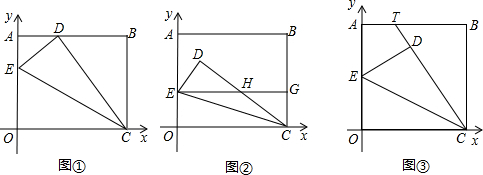
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。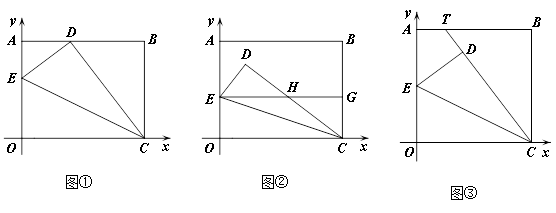
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。