题目内容
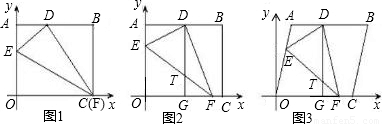
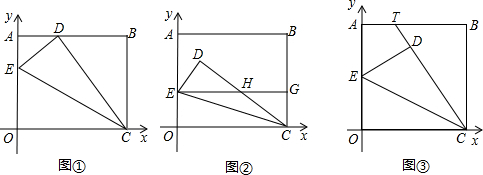
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在x轴和y轴上.在OA、OC边上选取适当的点E、F,连接EF,将△EOF沿EF折叠,使点O落在AB边上的点D处.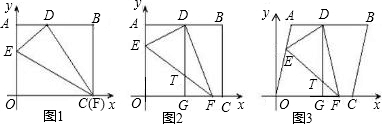
(1)如图1,当点F与点C重合时,OE的长度为
(2)如图2,当点F与点C不重合时,过点D作DG∥y轴交EF于点T,交OC于点G.求证:EO=DT;
(3)在(2)的条件下,设T(x,y),写出y与x之间的函数关系式为
(4)如图3,将矩形OABC变为平行四边形,放在平面直角坐标系中,且OC=10,OC边上的高等于8,点F与点C不重合,过点D作DG∥y轴交EF于点T,交OC于点G,求出这时T(x,y)的坐标y与x之间的函数关系式(不求自变量x的取值范围).
分析:(1)根据折叠的性质可得出DE=OE,OC=CD.
如果设出E点的坐标,可用E的纵坐标表示出AE、ED的长.
可根据相似三角形ADE和CDB得出的关于AE,BC,AD,BD的比例关系式求出E点的纵坐标.也就求出了E的坐标和OE的长.
(2)本题可通过证DT=OE来求出,如果连接OD,那么EF必垂直平分OD,如果设OD与EF的交点为P,那么OP=DP,△OEP≌△DPT,可得DT=OE;
(3)可先根据T的坐标表示出AD,AE,然后可在直角三角形ADE中表示出DE.而DE又可用AO-AE表示.可以此来求出y,x的函数关系式.
在(1)中给出的情况就是x的最小值的状况,可根据AD的长求出x的最小值,当x取最大值时,EF平分∠OAB,即E′与A重合,四边形EOGD为正方形,可据此求出此时x的值.有了x的最大和最小取值即可求出x的取值范围.
(4)的结论和(3)完全相同,求法也几乎完全一样.
如果设出E点的坐标,可用E的纵坐标表示出AE、ED的长.
可根据相似三角形ADE和CDB得出的关于AE,BC,AD,BD的比例关系式求出E点的纵坐标.也就求出了E的坐标和OE的长.
(2)本题可通过证DT=OE来求出,如果连接OD,那么EF必垂直平分OD,如果设OD与EF的交点为P,那么OP=DP,△OEP≌△DPT,可得DT=OE;
(3)可先根据T的坐标表示出AD,AE,然后可在直角三角形ADE中表示出DE.而DE又可用AO-AE表示.可以此来求出y,x的函数关系式.
在(1)中给出的情况就是x的最小值的状况,可根据AD的长求出x的最小值,当x取最大值时,EF平分∠OAB,即E′与A重合,四边形EOGD为正方形,可据此求出此时x的值.有了x的最大和最小取值即可求出x的取值范围.
(4)的结论和(3)完全相同,求法也几乎完全一样.
解答: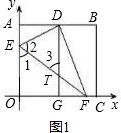 (1)5.
(1)5.
解:根据题意,运用勾股定理得BD=6,AD=4.
设OE=x,则DE=x,AE=8-x.
在Rt△ADE中,x2=(8-x)2+42,
解得x=5.即OE=5.
(2)证明:如图1,∵△EDF是由△EFO折叠得到的,
∴∠1=∠2.
又∵DG∥y轴,∠1=∠3.
∴∠2=∠3.
∴DE=DT.
∵DE=EO,
∴EO=DT.
(3)y=-
x2+4.
4<x≤8.
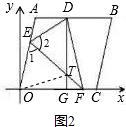
(4)解:如图2,连接OT,
由折叠性质可得OT=DT.
∵DG=8,TG=y,
∴OT=DT=8-y.
∵DG∥y轴,
∴DG⊥x轴.
在Rt△OTG中,∵OT2=OG2+TG2,
∴(8-y)2=x2+y2.
∴y=-
x2+4.
 (1)5.
(1)5.解:根据题意,运用勾股定理得BD=6,AD=4.
设OE=x,则DE=x,AE=8-x.
在Rt△ADE中,x2=(8-x)2+42,
解得x=5.即OE=5.
(2)证明:如图1,∵△EDF是由△EFO折叠得到的,
∴∠1=∠2.
又∵DG∥y轴,∠1=∠3.
∴∠2=∠3.
∴DE=DT.
∵DE=EO,
∴EO=DT.
(3)y=-
| 1 |
| 16 |
4<x≤8.

(4)解:如图2,连接OT,
由折叠性质可得OT=DT.
∵DG=8,TG=y,
∴OT=DT=8-y.
∵DG∥y轴,
∴DG⊥x轴.
在Rt△OTG中,∵OT2=OG2+TG2,
∴(8-y)2=x2+y2.
∴y=-
| 1 |
| 16 |
点评:本题主要考查了矩形和平行四边形的性质,三角形相似和全等,图形的翻折变换,二次函数的应用等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。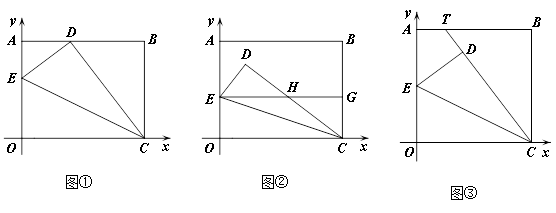
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。