题目内容
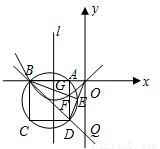
(2006•成都)如图,在平面直角坐标系中,已知点B(-2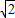 ,0),A(m,0)(-
,0),A(m,0)(-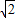 <m<0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连接BE与AD相交于点F.
<m<0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连接BE与AD相交于点F.(1)求证:BF=DO;
(2)设直线l是△BDO的边BO的垂直平分线,且与BE相交于点G.若G是△BDO的外心,试求经过B、F、O三点的抛物线的解析表达式;
(3)在(2)的条件下,在抛物线上是否存在点P,使该点关于直线BE的对称点在x轴上?若存在,求出所有这样的点的坐标;若不存在,请说明理由.
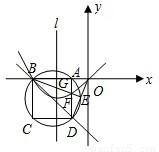
【答案】分析:(1)本题可通过全等三角形来证简单的线段相等,三角形ABF和ADO中,根据圆周角定理可得出∠ABF=∠ADO,已知了一组直角和AB=AD,因此两三角形全等,即可得出BF=OD的结论.
(2)如果G是三角形BDO的外心,根据三角形外心定义可知BE必垂直平分OD,因此三角形BOD是等腰三角形.在等腰直角三角形ABD中,BD=BO=2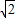 ,AB=OB-OA=2
,AB=OB-OA=2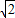 +m,因此可根据AB、BD的比例关系求出m的值,即可得出OA的长,而在(1)得出的全等三角形中,可得出OA=FG,据此可求出F点坐标.已知了B、F、O三点坐标,可用待定系数法求出抛物线的解析式.
+m,因此可根据AB、BD的比例关系求出m的值,即可得出OA的长,而在(1)得出的全等三角形中,可得出OA=FG,据此可求出F点坐标.已知了B、F、O三点坐标,可用待定系数法求出抛物线的解析式.
(3)在(2)中已经证得BE是∠OBD的角平分线,因此P点必为直线BD与抛物线的交点,先求出直线BD的解析式,然后联立抛物线的解析式可得出P点坐标.
解答:(1)证明:在△ABF和△ADO中,
∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠DAO=90°.
又∵∠ABF=∠ADO,
∴△ABF≌△ADO,
∴BF=DO.
(2)解:由(1),有△ABF≌△ADO,
∵AO=AF=m.
∴点F(m,m).
∵G是△BDO的外心,
∴点G在DO的垂直平分线上.
∴点B也在DO的垂直平分线上.
∴△DBO为等腰三角形,
∵AB=AD,
在Rt△BAD中,由勾股定理得:BO=BD= AB.
AB.
而|BO|=2 ,|AB|=|-2
,|AB|=|-2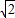 -m|=2
-m|=2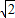 +m,
+m,
∴2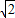 =
=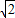 (2
(2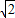 +m),
+m),
∴m=2-2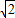 .
.
∴F(2-2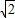 ,2-2
,2-2 ).
).
设经过B,F,O三点的抛物线的解析表达式为y=ax2+bx+c(a≠0).
∵抛物线过点O(0,0),
∴c=0.
∴y=ax2+bx. ①
把点B(-2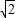 ,0),点F(2-2
,0),点F(2-2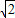 ,2-2
,2-2 )的坐标代入①中,
)的坐标代入①中,
得
即
解得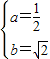
∴抛物线的解析表达式为y= x2+
x2+ x.②
x.②
(3)解:假定在抛物线上存在一点P,使点P关于直线BE的对称点P'在x轴上.
∵BE是∠OBD的平分线,
∴x轴上的点P'关于直线BE的对称点P必在直线BD上,
即点P是抛物线与直线BD的交点.
设直线BD的解析表达式为y=kx+b,并设直线BD与y轴交于点Q,则由△BOQ是等腰直角三角形.
∴|OQ|=|OB|.
∴Q(0,-2 ).
).
把点B(-2 ,0),点Q(0,-2
,0),点Q(0,-2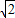 )代入y=kx+b中,
)代入y=kx+b中,
得
∴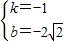
∴直线BD的解析表达式为y=-x-2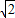 .
.
设点P(x,y),则有y=-x-2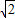 . ③
. ③
把③代入②,得 x2+
x2+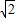 x=-x-2
x=-x-2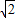 ,
,
∴ x2+(
x2+(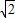 +1)x+2
+1)x+2 =0,
=0,
即x2+2(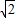 +1)x+4
+1)x+4 =0.
=0.
∴(x+2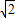 )(x+2)=0.
)(x+2)=0.
解得x=-2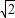 或x=-2.
或x=-2.
当x=-2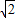 时,y=-x-2
时,y=-x-2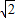 =2
=2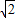 -2
-2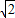 =0;
=0;
当x=-2时,y=-x-2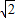 =2-2
=2-2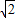 .
.
∴在抛物线上存在点P1(-2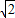 ,0),P2(-2,2-2
,0),P2(-2,2-2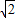 ),它们关于直线BE的对称点都在x轴上.
),它们关于直线BE的对称点都在x轴上.
点评:本题有一定的难度,综合性也比较强,有一定的新意,第3小问有些难度,有一定的能力要求,解这种题时需冷静地分析题意,找到切入点不会很难.
(2)如果G是三角形BDO的外心,根据三角形外心定义可知BE必垂直平分OD,因此三角形BOD是等腰三角形.在等腰直角三角形ABD中,BD=BO=2
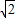 ,AB=OB-OA=2
,AB=OB-OA=2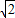 +m,因此可根据AB、BD的比例关系求出m的值,即可得出OA的长,而在(1)得出的全等三角形中,可得出OA=FG,据此可求出F点坐标.已知了B、F、O三点坐标,可用待定系数法求出抛物线的解析式.
+m,因此可根据AB、BD的比例关系求出m的值,即可得出OA的长,而在(1)得出的全等三角形中,可得出OA=FG,据此可求出F点坐标.已知了B、F、O三点坐标,可用待定系数法求出抛物线的解析式.(3)在(2)中已经证得BE是∠OBD的角平分线,因此P点必为直线BD与抛物线的交点,先求出直线BD的解析式,然后联立抛物线的解析式可得出P点坐标.
解答:(1)证明:在△ABF和△ADO中,
∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠DAO=90°.
又∵∠ABF=∠ADO,
∴△ABF≌△ADO,
∴BF=DO.
(2)解:由(1),有△ABF≌△ADO,
∵AO=AF=m.
∴点F(m,m).
∵G是△BDO的外心,
∴点G在DO的垂直平分线上.
∴点B也在DO的垂直平分线上.
∴△DBO为等腰三角形,
∵AB=AD,
在Rt△BAD中,由勾股定理得:BO=BD=
 AB.
AB.而|BO|=2
 ,|AB|=|-2
,|AB|=|-2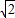 -m|=2
-m|=2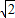 +m,
+m,∴2
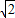 =
=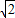 (2
(2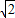 +m),
+m),∴m=2-2
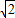 .
.∴F(2-2
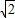 ,2-2
,2-2 ).
).设经过B,F,O三点的抛物线的解析表达式为y=ax2+bx+c(a≠0).
∵抛物线过点O(0,0),
∴c=0.
∴y=ax2+bx. ①
把点B(-2
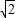 ,0),点F(2-2
,0),点F(2-2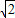 ,2-2
,2-2 )的坐标代入①中,
)的坐标代入①中,得

即

解得
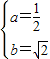
∴抛物线的解析表达式为y=
 x2+
x2+ x.②
x.②(3)解:假定在抛物线上存在一点P,使点P关于直线BE的对称点P'在x轴上.
∵BE是∠OBD的平分线,
∴x轴上的点P'关于直线BE的对称点P必在直线BD上,
即点P是抛物线与直线BD的交点.
设直线BD的解析表达式为y=kx+b,并设直线BD与y轴交于点Q,则由△BOQ是等腰直角三角形.
∴|OQ|=|OB|.
∴Q(0,-2
 ).
).
把点B(-2
 ,0),点Q(0,-2
,0),点Q(0,-2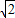 )代入y=kx+b中,
)代入y=kx+b中,得

∴
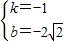
∴直线BD的解析表达式为y=-x-2
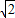 .
.设点P(x,y),则有y=-x-2
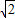 . ③
. ③把③代入②,得
 x2+
x2+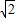 x=-x-2
x=-x-2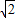 ,
,∴
 x2+(
x2+(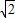 +1)x+2
+1)x+2 =0,
=0,即x2+2(
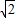 +1)x+4
+1)x+4 =0.
=0.∴(x+2
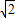 )(x+2)=0.
)(x+2)=0.解得x=-2
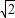 或x=-2.
或x=-2.当x=-2
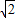 时,y=-x-2
时,y=-x-2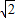 =2
=2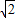 -2
-2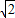 =0;
=0;当x=-2时,y=-x-2
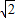 =2-2
=2-2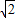 .
.∴在抛物线上存在点P1(-2
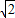 ,0),P2(-2,2-2
,0),P2(-2,2-2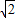 ),它们关于直线BE的对称点都在x轴上.
),它们关于直线BE的对称点都在x轴上.点评:本题有一定的难度,综合性也比较强,有一定的新意,第3小问有些难度,有一定的能力要求,解这种题时需冷静地分析题意,找到切入点不会很难.

练习册系列答案
相关题目
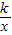 (k<0)的图象经过点A(-
(k<0)的图象经过点A(-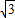 ,m),过点A作AB⊥x轴于点B,且△AOB的面积为
,m),过点A作AB⊥x轴于点B,且△AOB的面积为 .
.
 ,0),A(m,0)(-
,0),A(m,0)(-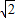 <m<0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连接BE与AD相交于点F.
<m<0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连接BE与AD相交于点F.
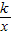 (k<0)的图象经过点A(-
(k<0)的图象经过点A(- ,m),过点A作AB⊥x轴于点B,且△AOB的面积为
,m),过点A作AB⊥x轴于点B,且△AOB的面积为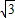 .
.