题目内容
 (1)已知:如图(1),∠AOB=90°,∠BOC=30°,分别作∠AOC,∠BOC的平分线OM、ON.求∠MON的度数;
(1)已知:如图(1),∠AOB=90°,∠BOC=30°,分别作∠AOC,∠BOC的平分线OM、ON.求∠MON的度数;
(2)如图(2)∠AOB=90°,将OC向下旋转,使∠BOC=30°,仍然分别作∠AOC,∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值,若不能,试说明理由.
解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=90°-30°=60°,
又∵OM、ON分别是∠AOC,∠BOC的平分线,
∴∠COM= ∠AOC=
∠AOC= ×60°=30°,
×60°=30°,
∠CON= ∠BOC=
∠BOC= ×30°=15°,
×30°=15°,
∴∠MON=∠COM+∠CON=30°+15°=45°;
(2)能.
∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°
又∵OM、ON分别是∠AOC,∠BOC的平分线,
∴∠COM= ∠AOC=
∠AOC= ×120°=60°,
×120°=60°,
∠CON= ∠BOC=
∠BOC= ×30°=15°,
×30°=15°,
∴∠MON=∠COM-∠CON=60°-15°=45°.
答:(1)∠MON的度数是45°;(2)能,其值是45°.
分析:根据图示,结合已知条件,分别求出∠COM和∠CON的度数,然后将其相加或相减,即可求出∠MON的度数.
点评:此题主要考查学生对角的计算的理解和掌握,此题难度不大,属于基础题,但是此题中涉及到两种情况,具有很好的代表性和典型性,是一道好题.
∴∠AOC=90°-30°=60°,
又∵OM、ON分别是∠AOC,∠BOC的平分线,
∴∠COM=
 ∠AOC=
∠AOC= ×60°=30°,
×60°=30°,∠CON=
 ∠BOC=
∠BOC= ×30°=15°,
×30°=15°,∴∠MON=∠COM+∠CON=30°+15°=45°;
(2)能.
∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°
又∵OM、ON分别是∠AOC,∠BOC的平分线,
∴∠COM=
 ∠AOC=
∠AOC= ×120°=60°,
×120°=60°,∠CON=
 ∠BOC=
∠BOC= ×30°=15°,
×30°=15°,∴∠MON=∠COM-∠CON=60°-15°=45°.
答:(1)∠MON的度数是45°;(2)能,其值是45°.
分析:根据图示,结合已知条件,分别求出∠COM和∠CON的度数,然后将其相加或相减,即可求出∠MON的度数.
点评:此题主要考查学生对角的计算的理解和掌握,此题难度不大,属于基础题,但是此题中涉及到两种情况,具有很好的代表性和典型性,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
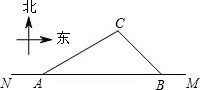 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.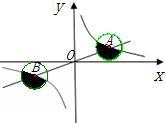 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为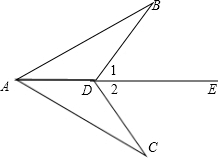 已知,如图,∠1=∠2,
已知,如图,∠1=∠2,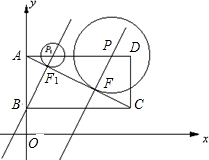 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧