题目内容
【题目】“端午”节前，第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干，放入不透明的盒中，此时随机取出火腿粽子的概率为
；妈妈发现小亮喜欢吃的火腿粽子偏少，第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中，这时随机取出火腿粽子的概率为
．
（1）请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只？
（2）若妈妈从盒中取出火腿粽子4只、豆沙粽子6只送爷爷和奶奶后，再让小亮从盒中不放回地任取2只，问恰有火腿粽子、豆沙粽子各1只的概率是多少？（用字母和数字表示豆沙粽子和火腿粽子，用列举法计算）
【答案】（1）第一次爸爸买了4只火腿粽子，8只豆沙粽子．（2）恰好火腿粽子、豆沙粽子各1只的概率为
．
【解析】
试题分析：（1）等量关系为：原来的火腿粽子数÷原来的总粽子数=
；后来的火腿粽子数÷后来的总粽子数=
；
（2）列举出所有情况，看所求的情况占所有情况的概率如何．
解：（1）设第一次爸爸买了x只火腿粽子，y只豆沙粽子．
则：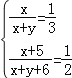
，
解得：
．
经检验得出：x+y≠0，x+y+6≠0，
∴x=4，y=8是原方程的根，
答：第一次爸爸买了4只火腿粽子，8只豆沙粽子．
（2）现在有火腿粽子9只，豆沙粽子9只，送给爷爷，奶奶后，还有火腿粽子5只，豆沙粽子3只．
记豆沙粽子a，b，c；火腿粽子1，2，3，4，5．恰好火腿粽子、豆沙粽子各1只的概率为
=．
第一次 第二次 | a | b | c | 1 | 2 | 3 | 4 | 5 |
a | （a，b） | （a，c） | （a，1） | （a，2） | （a，3） | （a，4） | （a，5） | |
b | （b，a） | （b，c） | （b，1） | （b，2） | （b，3） | （b，4） | （b，5） | |
c | （c，a） | （c，b） | （c，1） | （c，2） | （c，3） | （c，4） | （c，5） | |
1 | （1，a） | （1，b） | （1，c） | （1，2） | （1，3） | （1，4） | （1，5） | |
2 | （2，a） | （2，b） | （2，c） | （2，1） | （2，3） | （2，4） | （2，5） | |
3 | （3，a） | （3，b） | （3，c） | （3，1） | （3，2） | （3，4） | （3，5） | |
4 | （4，a） | （4，b） | （4，c） | （4，1） | （4，2） | （4，3） | （4，5） | |
5 | （5，a） | （5，b） | （5，c） | （5，1） | （5，2） | （5，3） | （5，4） |
阅读快车系列答案
