题目内容
【题目】如图,在等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底BC边上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=∠B.
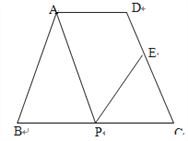
(1)求证:△ABP∽△PCE;
(2)求腰AB的长;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3.如果存在,求出BP的长;如果不存在,请说明理由。
【答案】(2)4cm(3)BP=1cm或BP=6cm
【解析】试题分析:(1)欲证△ABP∽△PCE,需找出两组对应角相等;由等腰梯形的性质可得出∠B=∠C,根据三角形外角的性质可证得∠EPC=∠BAP;由此得证;
(2)可过作AF⊥BC于F,由等腰梯形的性质得到AF是BC、AD差的一半,在Rt△ABF中,根据∠B的度数及BF的长即可求得AB的值;
(3)在(2)中求得了AB的长,即可求出DE:EC=5:3时,DE、CE的值.设BP的长为x,进而可表示出PC的长,然后根据(1)的相似三角形,可得出关于AB、BP、PC、CE的比例关系式,由此可得出关于x的分式方程,若方程有解,则x的值即为BP的长.若方程无解,则说明不存在符合条件的P点.
试题解析:证明:(1)∠BAP+∠BPA=120°
∠APB+∠CPE=120°
∴∠BAP=∠CPE
又∠ABP=∠PCE
∴△ABP∽△PCE
(2)过A、D分别作AG⊥BC,DH⊥BC
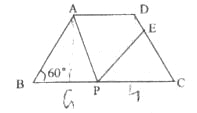
易得四边形AGHD是矩形
GH=AD=3cm
∴![]() cm
cm
在Rt△ABG中
![]() cm
cm
(3)由DE:EC=5:3
∴![]() ,
, ![]() .
.
又△ABP∽△PCE
∴![]()
即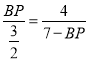
BP(7-BP)=6
BP=1cm或BP=6cm

练习册系列答案
相关题目