题目内容
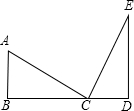如图，已知AB⊥BC，ED⊥BD，AB=CD，AC=CE．那么，AC与CE有何位置关系？说明理由．
解：AC⊥CE．
理由：∵AB⊥BC，ED⊥BD，
∴∠B=∠D=90°，
又AC=CE，
∴Rt△ABC≌Rt△CDE，
∴∠ACB=∠E，
∵∠DCE+∠E=90°，
∴∠CDCE+∠ACB=90°，
∴∠ACE=180°-∠ACB-∠DCE=180°-90°=90°，
∴AC⊥CE．
分析：由题中条件可得Rt△ABC≌Rt△CDE，即∠ACB=∠E，再由角之间的转化，即可得出结论．
点评：本题主要考查了全等三角形的判定及性质问题，应熟练掌握并能够求解一些简单的计算、证明问题．
理由：∵AB⊥BC，ED⊥BD，
∴∠B=∠D=90°，
又AC=CE，
∴Rt△ABC≌Rt△CDE，
∴∠ACB=∠E，
∵∠DCE+∠E=90°，
∴∠CDCE+∠ACB=90°，
∴∠ACE=180°-∠ACB-∠DCE=180°-90°=90°，
∴AC⊥CE．
分析：由题中条件可得Rt△ABC≌Rt△CDE，即∠ACB=∠E，再由角之间的转化，即可得出结论．
点评：本题主要考查了全等三角形的判定及性质问题，应熟练掌握并能够求解一些简单的计算、证明问题．
练习册系列答案
相关题目
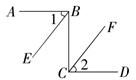22、如图，已知AB⊥BC，BC⊥CD，∠1=∠2．试判断BE与CF的关系，并说明你的理由．
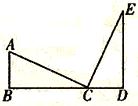22、如图，已知AB⊥BC，ED⊥BD，AB=CD，AC=CE．那么，AC与CE有何位置关系？说明理由．
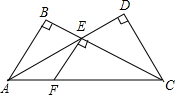如图，已知AB⊥BC，EF⊥BC，CD⊥AD，则有：
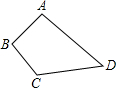如图，已知AB⊥BC，AB=3，BC=4，CD=12，DA=13，四边形ABCD的面积为
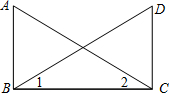如图，已知AB⊥BC于B，DC⊥BC于C，AB=DC，求证：∠1=∠2．