题目内容
在同一坐标平面中,正比例函数y=kx(k≠0)和二次函数y=kx2-4的图象可能是
- A.
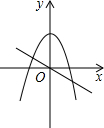
- B.
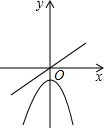
- C.
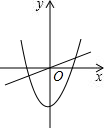
- D.

C
分析:先求出二次函数图象与y轴的交点,再根据正比例函数图象的特征与二次函数图象的特征,分k>0与k<0两种情况讨论求解.
解答:当x=0时,y=k×02-4=-4,
所以,二次函数图象与y轴的交点坐标为(0,-4),
①k>0时,正比例函数y=kx(k≠0)的图象经过第一、三象限,二次函数y=kx2-4的图象开口向上,
②k<0时,正比例函数y=kx(k≠0)的图象经过第二、四象限,二次函数y=kx2-4的图象开口向下,
纵观各选项,只有C选项符合.
故选C.
点评:本题考查了二次函数图象,正比例函数图象,主要利用了二次函数图象与y轴的交点坐标,开口方向以及一次函数图象的k值与经过的象限之间的关系.
分析:先求出二次函数图象与y轴的交点,再根据正比例函数图象的特征与二次函数图象的特征,分k>0与k<0两种情况讨论求解.
解答:当x=0时,y=k×02-4=-4,
所以,二次函数图象与y轴的交点坐标为(0,-4),
①k>0时,正比例函数y=kx(k≠0)的图象经过第一、三象限,二次函数y=kx2-4的图象开口向上,
②k<0时,正比例函数y=kx(k≠0)的图象经过第二、四象限,二次函数y=kx2-4的图象开口向下,
纵观各选项,只有C选项符合.
故选C.
点评:本题考查了二次函数图象,正比例函数图象,主要利用了二次函数图象与y轴的交点坐标,开口方向以及一次函数图象的k值与经过的象限之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
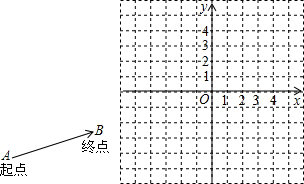
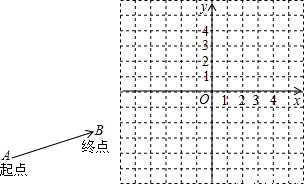
 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为| |.显然,有向线段
|.显然,有向线段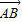 和有向线段
和有向线段 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段. ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|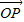 |=3.
|=3.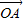 有向线段,使得
有向线段,使得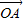 =3
=3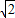 ,
,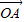 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;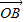 的终点B的坐标为(3,
的终点B的坐标为(3,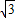 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角; 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
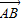 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|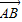 |.显然,有向线段
|.显然,有向线段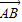 和有向线段
和有向线段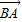 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.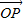 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|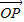 |=3.
|=3.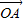 有向线段,使得
有向线段,使得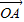 =3
=3 ,
, 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;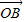 的终点B的坐标为(3,
的终点B的坐标为(3, ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;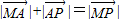 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)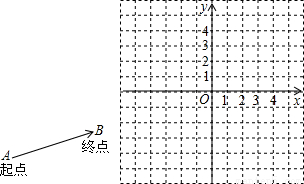
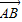 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|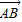 |.显然,有向线段
|.显然,有向线段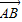 和有向线段
和有向线段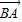 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.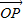 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|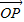 |=3.
|=3.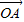 有向线段,使得
有向线段,使得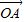 =3
=3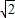 ,
,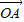 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;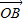 的终点B的坐标为(3,
的终点B的坐标为(3,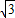 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;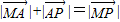 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)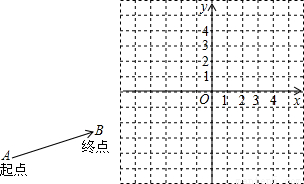
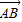 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|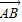 |.显然,有向线段
|.显然,有向线段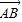 和有向线段
和有向线段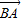 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.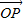 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|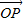 |=3.
|=3.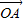 有向线段,使得
有向线段,使得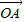 =3
=3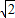 ,
,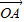 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;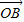 的终点B的坐标为(3,
的终点B的坐标为(3,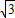 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;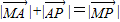 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)