题目内容
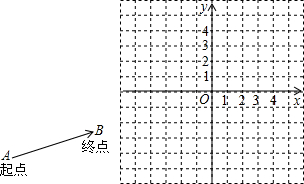
先阅读短文,再解答短文后面的问题.规定了方向的线段称为有向线段.比如,对于线段AB,规定以A为起点,B为终点,便可得到一条从A到B的有向线段.为强调其方向,我们在其终点B处画上箭头(如下图-1).以A为起点,B为终点的有向线段记为
| AB |
| AB |
| AB |
| BA |
对于同一平面内的有向线段,我们可以在该平面建立直角坐标系进行研究(一般情况,直角坐标系的单位长度与有向线段的单位长度相同).比如,以坐标原点O(0,0)为起点,P(3,0)为终点的有向线段
| OP |
| OP |
问题:
(1)在如图所示的平面直角坐标系中画出
| OA |
| OA |
| 2 |
| OA |
(2)若有向线段
| OB |
| 3 |
(3)若点M、A、P在同一直线上,|
| MA |
| AP |
| MP |
分析:(1)根据定义,只需作出点A(3,-3)即可;
(2)根据定义运用勾股定理根据它的坐标求得它的模,根据正切值求得夹角;
(3)注意由于三点的位置顺序不确定,显然不一定成立.
(2)根据定义运用勾股定理根据它的坐标求得它的模,根据正切值求得夹角;
(3)注意由于三点的位置顺序不确定,显然不一定成立.
解答:解:(1)见图
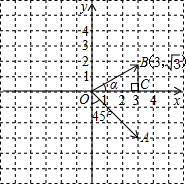
(2)在平面直角坐标系中画出
,过B作BC⊥x轴于C.
在Rt△OCB中,由勾股定理知:|
|=2
设
与x轴正半轴的夹角为α.α=30°
即
的模为2
,
与x轴正半轴的夹角为30°.
(3)若点M、A、P在同一直线上,|
|+|
|=|
|不一定成立.
如图甲:|
|+|
|=|
|成立.
如图乙:|
|+|
|=|
|不成立.


(2)在平面直角坐标系中画出
| OB |
在Rt△OCB中,由勾股定理知:|
| OB |
| 3 |
设
| OB |
即
| OB |
| 3 |
| OB |
(3)若点M、A、P在同一直线上,|
| MA |
| AP |
| MP |
如图甲:|
| MA |
| AP |
| MP |
如图乙:|
| MA |
| AP |
| MP |

点评:此题要正确理解定义,能够综合运用勾股定理和锐角三角函数分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 .
.
 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序: 为始点,
为始点, 为终点,我们就说线段
为终点,我们就说线段 具有射线的
具有射线的 ,线段
,线段 。
。
 (有向线段与
(有向线段与 轴的长度单位相同),
轴的长度单位相同), ,
,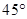 ,且与
,且与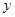 轴的正半轴的夹角是
轴的正半轴的夹角是 的终点
的终点 ),求它的模及它与
),求它的模及它与 的度数。
的度数。 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序: 为始点,
为始点, 为终点,我们就说线段
为终点,我们就说线段 具有射线的
具有射线的 ,线段
,线段 。
。
 (有向线段与
(有向线段与 轴的长度单位相同),
轴的长度单位相同), ,
, ,且与
,且与 轴的正半轴的夹角是
轴的正半轴的夹角是 的终点
的终点 ),求它的模及它与
),求它的模及它与 的度数。
的度数。