��Ŀ����
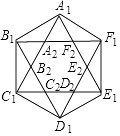
����Ŀ����ͼ��һ������ʽ�������ʾ��ͼ�����峤AB=50cm����������쳤����BC=30cm������A��B��C��ͬһ��ֱ���ϣ���������ĵ�װ��һԲ�ι��֡�A����ֱ��Ϊ10cm����A��ˮƽ�������ڵ�D����A��AE��DM�����˵�����Ȼ�´���������ʱ���˸о���Ϊ�������֪ij�˵�����Ȼ�´��ڵ�C�������˴ﵽ����������ʱ����C����ˮƽ���棨40 ![]() +5��cm�����ʱ��������ˮƽ��AE���ɽǡ�CAE�Ĵ�С����B��ˮƽ����ľ��룮
+5��cm�����ʱ��������ˮƽ��AE���ɽǡ�CAE�Ĵ�С����B��ˮƽ����ľ��룮 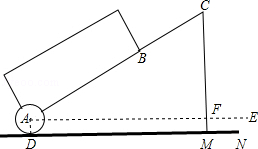
���𰸡��⣺CF=40 ![]() +5��5=40
+5��5=40 ![]() ��m���� ��sin��CAF=
��m���� ��sin��CAF= ![]() =
= ![]() ��
��
���CAF=60�㣬
��ͼ��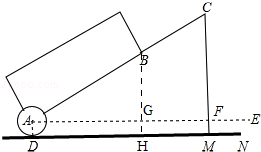
��BH��AF�ڵ�G����DM�ڵ�H��
��BG��CF��
���ABG�ס�ACF��![]() ��
��
�� ![]() ��
��
��ã�BG=25 ![]() ��
��
��B��ˮ����ľ���Ϊ��25 ![]() +5 ��cm
+5 ��cm
���������������Ǻ��������CAF���������������εó�����ʽ���BG�����ɣ�
�����㾫����������Ҫ���������ߵ����ʶ��������������ε�Ӧ�õ����֪ʶ�㣬��Ҫ�������ߵ����ʣ�1�������е㴹ֱ�������뾶��ֱ����Բ������2�������е㴹ֱ�����ߵ�ֱ�߱ؾ���Բ��3��Բ�����ߴ�ֱ�ھ����е�İ뾶����ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������������ȷ�����⣮

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�