题目内容
（2013•潍坊二模）已知四边形ABCD，对角线AC与BD互相垂直．顺次连接其四条边的中点，得到新四边形的形状一定是（ ）
分析：根据四边形对角线互相垂直，运用三角形中位线平行于第三边证明四个角都是直角，判断是矩形．
解答：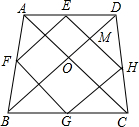
解：如图：∵E、F、G、H分别为各边中点
∴EF∥GH∥DB，EF=GH=
DB
EH=FG=
AC，EH∥FG∥AC
∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形．
故选B．
解：如图：∵E、F、G、H分别为各边中点∴EF∥GH∥DB，EF=GH=
| 1 |
| 2 |
EH=FG=
| 1 |
| 2 |
∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形．
故选B．
点评：本题考查的是中点四边形，解题时，主要是利用了三角形中位线定理的性质，比较简单，也可以利用三角形的相似，得出正确结论．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
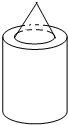（2013•潍坊二模）如图，组合体的俯视图是（ ）
（2013•潍坊二模）如图，AB的中垂线为CP交AB于点P，且AC=2CP．甲、乙两人想在AB上取D、E两点，使得AD=DC=CE=EB，其作法如下：甲作∠ACP、∠BCP的角平分线，分别交AB于D、E两点，则D、E即为所求；乙作AC、BC的中垂线，分别交AB于D、E两点，则D、E即为所求．对于甲、乙两人的作法，下列正确的是（ ）