题目内容
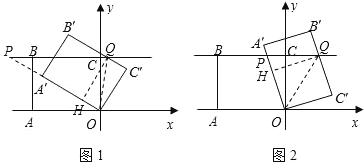
【题目】如图，在平面直角坐标系中，0为坐标原点，点A的坐标为（－4，0），直线BC经过点B（－4，3），C（0，3），将四边形OABC绕点O按顺时针方向旋转α度（0＜α≤l80°）得到四边形OA′B′C′，此时直线OA′、直线B′C′，分别与直线BC相交于P，Q．在四边形OABC旋转过程中，若BP=
BQ 则点P的坐标为__________．
【答案】
或
【解析】试题解析：过点Q作QH⊥OA′于H,连接OQ,则QH=OC′=OC，
∴PQ=OP.
设BP=x，
∴BQ=2x，
如图1,当点P在点B左侧时,
OP=PQ=BQ+BP=3x，
在Rt△PCO中, 
解得
(不符实际,舍去).
如图2，当点P在点B右侧时，
∴OP=PQ=BQBP=x，PC=4x.
在Rt△PCO中, 
解得
综上可知,点
,
使
故答案为： 
或
.
练习册系列答案
相关题目
