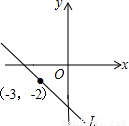题目内容
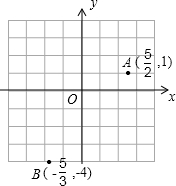 如图,坐标平面上有A(
如图,坐标平面上有A(| 5 |
| 2 |
| 5 |
| 3 |
| A、(3,-1) | ||
| B、(1,2) | ||
C、(0,
| ||
| D、(0,-2) |
分析:先求出直线L的解析式,再分别求出(3,-1),(1,2),(0,
),(0,-2)到直线L的距离,比较后即可得出.
| 1 |
| 2 |
解答:解:将A(
,1)、B(-
,-4)两点代入y=kx+b,则有
,
解得
.
故直线L的解析式为y=
x-2.
∴(3,-1)到直线L的距离为:
×
×
÷(
×
)=
;
同理(1,2)到直线L的距离为:
;
(0,
)到直线L的距离为:
;
(0,-2)到直线L的距离为:0,在直线L上.
故选D.
| 5 |
| 2 |
| 5 |
| 3 |
|
解得
|
故直线L的解析式为y=
| 6 |
| 5 |
∴(3,-1)到直线L的距离为:
| 1 |
| 2 |
| 13 |
| 5 |
| 13 |
| 6 |
| 1 |
| 2 |
(
|
13
| ||
| 61 |
同理(1,2)到直线L的距离为:
14
| ||
| 61 |
(0,
| 1 |
| 2 |
35
| ||
| 821 |
(0,-2)到直线L的距离为:0,在直线L上.
故选D.
点评:本题考查了待定系数法求函数解析式,及直线外一点到直线的距离的求法,难度较大.

练习册系列答案
相关题目
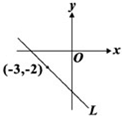 9、如图的坐标平面上,有一条通过点(-3,-2)的直线L.若四点(-2,a)、(0,b)、(c,0)、(d,-1)在L上,则下列数值的判断,何者正确( )
9、如图的坐标平面上,有一条通过点(-3,-2)的直线L.若四点(-2,a)、(0,b)、(c,0)、(d,-1)在L上,则下列数值的判断,何者正确( ) 如图,坐标平面上有A(
如图,坐标平面上有A( ,1)、B(-
,1)、B(- ,-4)两点.过A、B两点作直线L后,则下列与直线L距离最短的点是
,-4)两点.过A、B两点作直线L后,则下列与直线L距离最短的点是 )
)