题目内容
【题目】如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2. 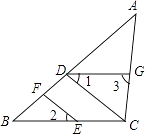
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?
【答案】
(1)解:DG∥BC.
理由:∵CD∥EF,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC
(2)解:CD⊥AB.
理由:∵由(1)知DG∥BC,∠3=85°,
∴∠BCG=180°﹣85°=95°.
∵∠DCE:∠DCG=9:10,
∴∠DCE=95°× ![]() =45°.
=45°.
∵DG是∠ADC的平分线,
∴∠ADC=2∠CDG=90°,
∴CD⊥AB
【解析】(1)先根据CD∥EF得出∠2=∠BCD,再由∠1=∠2得出∠1=∠BCD,进而可得出结论;(2)根据DG∥BC,∠3=85°得出∠BCG的度数,再由∠DCE:∠DCG=9:10得出∠DCE的度数,由DG是∠ADC的平分线可得出∠ADC的度数,由此得出结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目