题目内容
如图,一条直线过点A(0,4),B(2,0),将这条直线向左平移与x轴、y轴的负半轴分别交于点C、D,使DB=DC.
(1)求直线CD的函数解析式;
(2)求△BCD的面积;
(3)在直线AB或直线CD上是否存在点P,使△PBC的面积等于△BCD的面积的2倍?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

(1)求直线CD的函数解析式;
(2)求△BCD的面积;
(3)在直线AB或直线CD上是否存在点P,使△PBC的面积等于△BCD的面积的2倍?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

解:
(1)∵DB=DC,BC⊥OD,
∴OC=OB,
∵B(2,0),
∴C(-2,0),
∵OC=OB,∠AOB=∠DOC,∠ABO=∠DCO,
∴△ABO∽△DCO,
∴OA=OD,
∴D(0,-4),
设直线CD的函数解析式:y=ax+b,代入得
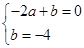
解得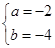
直线CD:y=2x-4;
(2)△BCD的面积是:S=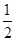 ×BC×OD=
×BC×OD=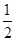 ×(2+2)×4=8,
×(2+2)×4=8,
∴△BCD的面积是8;
(3)存在,直线AB上:(-2,8)、(6,-8);直线CD上:(-6,8)、(2,-8).
(1)∵DB=DC,BC⊥OD,
∴OC=OB,
∵B(2,0),
∴C(-2,0),
∵OC=OB,∠AOB=∠DOC,∠ABO=∠DCO,
∴△ABO∽△DCO,
∴OA=OD,
∴D(0,-4),
设直线CD的函数解析式:y=ax+b,代入得
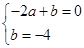
解得
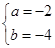
直线CD:y=2x-4;
(2)△BCD的面积是:S=
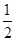 ×BC×OD=
×BC×OD=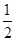 ×(2+2)×4=8,
×(2+2)×4=8,∴△BCD的面积是8;
(3)存在,直线AB上:(-2,8)、(6,-8);直线CD上:(-6,8)、(2,-8).
先证明△ABO∽△DCO求出D的坐标,利用已知两点求出直线CD的解析式,再利用面积公式求出点的坐标.

练习册系列答案
相关题目
 >1时,
>1时, 的取值范围(直接写答案);
的取值范围(直接写答案);
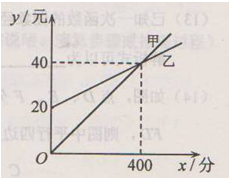

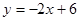 与两坐标轴围城的三角形面积是________.
与两坐标轴围城的三角形面积是________. :
: 与直线
与直线 :
: 相交于点
相交于点 ,直线
,直线 轴交于点
轴交于点 ,平行于
,平行于 分别交直线
分别交直线 、
、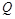 两点(点
两点(点 上,在
上,在 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点 ,设
,设 重叠部分的面积为
重叠部分的面积为 ,求
,求 的函数关系式;并注明
的函数关系式;并注明

 元时,销售量为
元时,销售量为 千克;
千克; 中,
中, 随
随 的增大而减小,则
的增大而减小,则 的取值范围是_____________。
的取值范围是_____________。