题目内容
已知抛物线y=x2+mx-
m2(m>0).
(1)求证:该抛物线与x轴必有两个交点;
(2)若抛物线与x轴的两个交点分别为A、B(点A在点B的左侧),且AB=4,求m的值;
(3)在条件(2)的前提下,y轴上是否存在点C,使得△ABC为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
| 3 | 4 |
(1)求证:该抛物线与x轴必有两个交点;
(2)若抛物线与x轴的两个交点分别为A、B(点A在点B的左侧),且AB=4,求m的值;
(3)在条件(2)的前提下,y轴上是否存在点C,使得△ABC为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
分析:(1)令y=0,利用根的判别式证明即可;
(2)令y=0,解关于x的一元二次方程求出A、B的坐标,然后表示出AB,即可得到m的值;
(3)判断出△AOC和△COB相似,利用相似三角形对应边成比例列式求出OC的长,再分点C在y轴负半轴和正半轴两种情况写出即可.
(2)令y=0,解关于x的一元二次方程求出A、B的坐标,然后表示出AB,即可得到m的值;
(3)判断出△AOC和△COB相似,利用相似三角形对应边成比例列式求出OC的长,再分点C在y轴负半轴和正半轴两种情况写出即可.
解答:(1)证明:令y=0,则x2+mx-
m2=0,
△=b2-4ac=m2-4×1×(-
m2)=2m2,
∵m>0,
∴△>0,
∴该抛物线与x轴必有两个交点;
(2)解:令y=0,则x2+mx-
m2=0,
解得x1=-
m,x2=
,
∵点A在点B的左侧,
∴A(-
m,0),B(
,0),
∴AB=
-(-
m)=2m=4,
解得m=2;
(3)存在.
理由如下:由(2)得,m=2,点A(-3,0),B(1,0),
∵△ABC为直角三角形,点C在y轴上,
∴∠ACB=90°,
∴△AOC∽△COB,
∴
=
,
即
=
,
解得OC=
,
点C在y轴负半轴时,点C的坐标为(0,-
),
点C在y轴正半轴时,点C的坐标为(0,
),
综上所述,y轴上有点C的坐标(0,-
),(0,
),使得△ABC为直角三角形.
| 3 |
| 4 |
△=b2-4ac=m2-4×1×(-
| 3 |
| 4 |
∵m>0,
∴△>0,
∴该抛物线与x轴必有两个交点;
(2)解:令y=0,则x2+mx-
| 3 |
| 4 |
解得x1=-
| 3 |
| 2 |
| m |
| 2 |
∵点A在点B的左侧,
∴A(-
| 3 |
| 2 |
| m |
| 2 |
∴AB=
| m |
| 2 |
| 3 |
| 2 |
解得m=2;
(3)存在.
理由如下:由(2)得,m=2,点A(-3,0),B(1,0),
∵△ABC为直角三角形,点C在y轴上,
∴∠ACB=90°,
∴△AOC∽△COB,
∴
| OA |
| OC |
| OC |
| OB |
即
| 3 |
| OC |
| OC |
| 1 |
解得OC=
| 3 |
点C在y轴负半轴时,点C的坐标为(0,-
| 3 |
点C在y轴正半轴时,点C的坐标为(0,
| 3 |
综上所述,y轴上有点C的坐标(0,-
| 3 |
| 3 |
点评:本题是二次函数综合题型,主要利用了根的判别式,抛物线与x轴的交点问题,相似三角形的判定与性质,综合题,但难度不大,(3)点C的坐标要分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
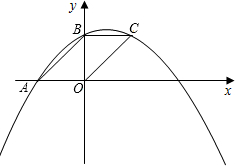 (1)求b+c的值;
(1)求b+c的值;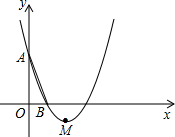 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.