题目内容
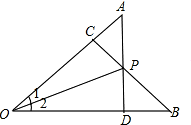 如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是
如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是
- A.∠1=∠2
- B.∠1>∠2
- C.∠1<∠2
- D.无法确定
A
分析:认真读已知条件,找准已知在图形上的位置,可发现△ACP≌△BDP,得线段相等,然后根据角平分线上的任意一点到角的两边距离相等判断.
解答:∵AD⊥OB,BC⊥OA,
∴∠ACP=∠BDP,∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP
∴CP=DP
∴OP是角AOB的平分线,
∴∠1=∠2.
故选A.
点评:本题考查了三角形全等的判定和性质;主要先利用全等三角形证明CP=DP,再由角平分线的逆定理可知OP是角AOB的平分线,由判定可知∠1=∠2.
分析:认真读已知条件,找准已知在图形上的位置,可发现△ACP≌△BDP,得线段相等,然后根据角平分线上的任意一点到角的两边距离相等判断.
解答:∵AD⊥OB,BC⊥OA,
∴∠ACP=∠BDP,∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP
∴CP=DP
∴OP是角AOB的平分线,
∴∠1=∠2.
故选A.
点评:本题考查了三角形全等的判定和性质;主要先利用全等三角形证明CP=DP,再由角平分线的逆定理可知OP是角AOB的平分线,由判定可知∠1=∠2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 12、如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
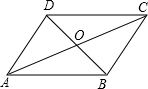
12、如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( ) 9、如图所示,OD=OB,AD∥BC,则全等三角形有( )
9、如图所示,OD=OB,AD∥BC,则全等三角形有( )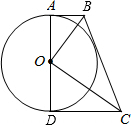 如图所示,AD是⊙O的直径,AB、CD与⊙O相切于点A和点D.
如图所示,AD是⊙O的直径,AB、CD与⊙O相切于点A和点D.