题目内容
【题目】我们把1°的圆心角所对的弧叫做1°的弧.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,已知,![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() .
.
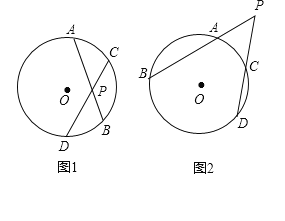
(1)如图1,⊙O的两条弦AB、CD相交于圆内一点P,求证:![]() ;
;
(2)如图2,⊙O的两条弦AB、CD延长线相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论,并证明.
【答案】(1)见解析;(2)问题(1)中的结论不成立,图2的结论为![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接BC,由题意可知∠B=![]() ,∠C=
,∠C=![]() ,再由三角形的外角性质即可得证;
,再由三角形的外角性质即可得证;
(2)连接BC,同理可得∠ABC=![]() ,∠C=
,∠C=![]() ,再由三角形的外角性质可得结论.
,再由三角形的外角性质可得结论.
证明:(1)连接BC,如下图所示,

∵∠B是![]() 所对的圆周角,∠C是
所对的圆周角,∠C是![]() 所对的圆周角,
所对的圆周角,
∴∠B=![]() ,∠C=
,∠C=![]()
∵∠APC是△BCP的外角,
∴∠APC=∠B+∠C=![]()
(2)问题(1)中的结论不成立,图2的结论为![]() ,理由如下:
,理由如下:
连接BC,如下图所示,

同理可得∠ABC=![]() ,∠C=
,∠C=![]() ,
,
∵∠ABC是△BCP的外角,
∴∠ABC=∠APC+∠C,
∴∠APC=∠ABC-∠C=![]()

练习册系列答案
相关题目