题目内容
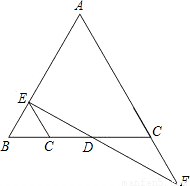
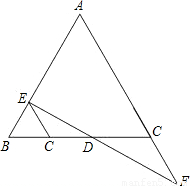
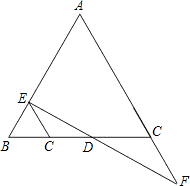 (A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
(A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
①AB=AC;②BD=CD;③BE=CF
已知:DE⊥AB、DF⊥AC,垂足分别为E、F,AB=AC,BD=CD
求证:BE=CF
已知:DE⊥AB、DF⊥AC,垂足分别为E、F,AB=AC,BE=CF
求证:BD=CD
已知:DE⊥AB、DF⊥AC,垂足分别为E、F,BD=CD,BE=CF
求证:AB=AC
(B类)如图,EG∥AF,请你从下面三个条件中,再选两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
①AB=AC;②DE=DF;③BE=CF
已知:EG∥AF,AB=AC,DE=DF
求证:BE=CF
友情提醒:若两题都做的同学,请你确认以哪类题记分,你的选择是A类类题.
解:(A类)
已知:…,AB=AC,BD=CD
求证:BE=CF.
证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
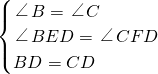
∴△BDE≌△CDF.
∴BE=CF.
已知:…,AB=AC,DE=DF,
求证:BE=CF.
证明:∵EG∥AF,
∴∠GED=∠F,
∠BGE=∠BCA.
∵AB=AC,
∴∠B=∠BCA,
∴∠B=∠BGE,
∴BE=EG.
在△DEG和△DFC中
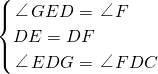
∴△DEG≌△DFC,
∴EG=CF,
∴BE=CF.
分析:本题是开放题,应先确定选择哪对三角形,对应三角形全等条件求解;再根据全等三角形的性质得出结论.
点评:这是一道考查三角形全等的识别方法的开放性题目,答案可有多种.同时还考查了全等三角形的性质.
已知:…,AB=AC,BD=CD
求证:BE=CF.
证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在△BDE和△CDF中
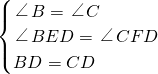
∴△BDE≌△CDF.
∴BE=CF.
已知:…,AB=AC,DE=DF,
求证:BE=CF.
证明:∵EG∥AF,
∴∠GED=∠F,
∠BGE=∠BCA.
∵AB=AC,
∴∠B=∠BCA,
∴∠B=∠BGE,
∴BE=EG.
在△DEG和△DFC中
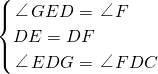
∴△DEG≌△DFC,
∴EG=CF,
∴BE=CF.
分析:本题是开放题,应先确定选择哪对三角形,对应三角形全等条件求解;再根据全等三角形的性质得出结论.
点评:这是一道考查三角形全等的识别方法的开放性题目,答案可有多种.同时还考查了全等三角形的性质.

练习册系列答案
相关题目
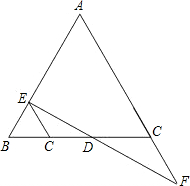 (A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
(A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).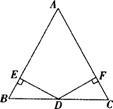 22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).