题目内容
【题目】已知![]() 中,
中,![]() ,M是BC的中点.如图.
,M是BC的中点.如图.
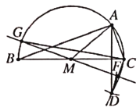
(1)以M为圆心.MB为半径,作半圆M﹔
(2)分别以B,C为圆心,BA,CA为半径作弧,两弧交于点D;
(3)连接AM,AD,CD;
(4)作线段CD的中垂线,分别交线段CD于点F,半圆M于点G,连接GC;
(5)以点G为圆心,线段GC为半径,作![]() .
.
根据以上作图过程及所作图形,下列结论中:
①点A在半圆M上;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() .一定正确的是________.
.一定正确的是________.
【答案】①②④
【解析】
根据圆周角定理,弧、弦、圆心角的关系定理,相似三角形的判定方法,以及其他与圆有关的性质及定理即可判断.
解:由作图可知,以M为圆心,BC为直径的半圆是![]() 的外接圆,
的外接圆,
∵∠BAC=90°,
∴∠BAC是直径所对的圆周角
∴点A在半圆M上,故①正确;
由分别以B,C为圆心,BA,CA为半径作弧,两弧交于点D可知,
CA、CD是以圆C的半径,
∴![]() ,故②正确;
,故②正确;
∵![]() 在以M为圆心、BM为半径的圆中,
在以M为圆心、BM为半径的圆中,![]() 在以B为圆心、BA为半径的圆中,
在以B为圆心、BA为半径的圆中,
∴![]() ,故③错误;
,故③错误;
∵AM=BM,AC=CD,
∴∠ABM=∠BAM,∠ADC=∠DAC
又∠BAC=∠ABM+∠ACB=90°,
∠AFC=∠CAF+∠ACF=90°
∴∠ABM=∠DAC
∴∠MAB=∠ADC,∠AMB=∠ACD
∴△AMB∽△ADC,故④正确;
在以点M为圆心、BC为直径的圆中,BC是直径,CG是该圆的一条弦,
∴BC>CG ,即BC≠CG,故⑤错误;
∵作线段CD的中垂线,
∴CF=![]() CD=AC,
CD=AC,
∴∠CGF=![]() ∠ABC=
∠ABC=![]() ∠BAM,
∠BAM,
∴∠CGF≠∠BAM,故⑥错误,
综上所述:①②④正确,
故答案为:①②④.

【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.
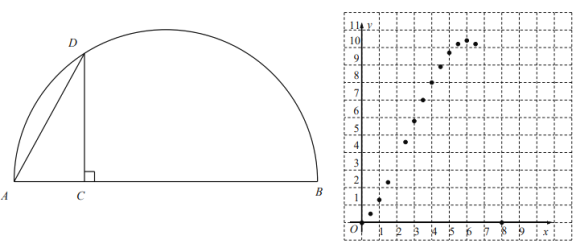
【题目】如图,在半![]() 中,P是直径AB上一动点,且
中,P是直径AB上一动点,且![]() ,过点P作
,过点P作![]() 交半
交半![]() 于点C,P为垂足,连接BC,过点P作
于点C,P为垂足,连接BC,过点P作![]() 于点D.
于点D.
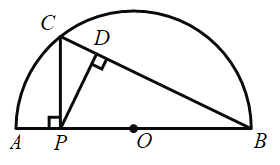
小明根据学习函数的经验,对线段AP,CP,PD的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于动点P在AB上的不同位置,画图,测量,得到了线段AP,CP,PD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | 位置10 | |
| 0.37 | 0.88 | 1.59 | 2.01 | 2.44 | 3.00 | 3.58 | 4.37 | 5.03 | 5.51 |
| 1.45 | 2.12 | 2.65 | 2.83 | 2.95 | 3.00 | 2.95 | 2.67 | 2.21 | 1.65 |
| 1.40 | 1.96 | 2.27 | 2.31 | 2.27 | 2.13 | 1.87 | 1.39 | 0.89 | 0.48 |
在AP,CP,PD的长度这三个量中,确定________的长度是自变量, ________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
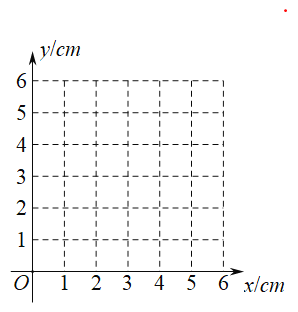
(3)结合函数图象,解决问题:当![]() 时,AP的长度约为________.
时,AP的长度约为________.