题目内容
【题目】如图1,在平面直角坐标系中,点![]() ,点
,点![]() ,以
,以![]() 为边在右侧作正方形
为边在右侧作正方形![]()

(1)当点![]() 在
在![]() 轴正半轴上运动时,求点
轴正半轴上运动时,求点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)当![]() 时,如图2,
时,如图2,![]() 为
为![]() 上一点,过点
上一点,过点![]() 作
作![]() ,
,![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
(3)如图3,在第(2)问的条件下,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,作
上的点,作![]() 轴交
轴交![]() 于
于![]() ,作
,作![]() 轴交
轴交![]() 于
于![]() ,
,![]() 是
是![]() 与
与![]() 的交点,若
的交点,若![]() ,试确定
,试确定![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
【答案】(1)C(m+4,m);(2)4![]() ;(3)45°,证明见解析
;(3)45°,证明见解析
【解析】
(1)如图1中,作CE⊥x轴于E.利用全等三角形的性质即可解决问题;
(2)如图2中,作ME⊥y轴于E,作MF∥OA交OD于F.构造平行四边形,全等三角形解决问题即可;
(3)如图3中,延长CO到M,使得OM=DE.则△AOM≌△ADE.设AG=a,AH=b,由题意DE=a,OF=b,EK=DH=4-b,EC=OG=4-a,利用勾股定理想办法证明EF=OF+DE=FM,再证明△AFM≌△AFE,可得∠FAM=![]() 即可解决问题.
即可解决问题.
解:(1)如图1中,作CE⊥x轴于E.
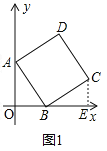
∵∠AOB=∠ABC=∠CEB=90°,
∴∠ABO+∠OAB=90°,∠ABO+∠CBE=90°,
∴∠OAB=∠CBE,∵AB=BC,
∴△ABO≌△BCE,
∴CE=OB=m,BE=OA=4,
∴C(m+4,m).
(2)如图2中,作ME⊥y轴于E,作MF∥OA交OD于F.
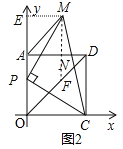
∵∠MEP=∠MPC=∠COP=90°,
∴∠MPE+∠PME=90°,∠MAE+∠CPO=90°,
∴∠PME=∠CPO,∵PM=PC,
∴△MEP≌△OPC,
∴PE=OC=AO,EM=OP,
∴OP=AE=EM,
∴∠EAM=45°,∵∠AOD=45°,
∴∠EAM=∠AOD,
∴AM∥ON,∵OA∥MF,
∴四边形AMFO是平行四边形,
∴FM=OA=CD,MF∥CD,AM=OF,
∴∠NDC=∠NFM,∵∠MNF=∠CND,
∴△CDN≌△MFN,
∴FN=DN,
∴AM+2DN=OF+DF=OD=4![]() .
.
(3)如图3中,延长CO到M,使得OM=DE.则△AOM≌△ADE.
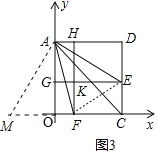
设AG=a,AH=b,由题意DE=a,OF=b,EK=DH=4-b,EC=OG=4-a,
∵S四边形KFCE=2S四边形AGKH,
∴(4-a)(4-b)=2ab,
∴16-4(a+b)+ab=2ab,
∴ab=16-4(a+b),
∴2ab=32-8(a+b),
在Rt△EFC中,EF=![]()
∴EF=OF+DE=OF+OM=FM,
∵AF=AF,AM=AE,
∴△AFM≌△AFE,
∴∠FAM=∠FAE,
∵∠DAE=∠OAM,
∴∠EAM=∠DAO=90°,
∴∠EAF=45°.