题目内容
(2012•东莞模拟)阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:
(1)(5+i)(3-4i)=5×3+5×(-4i)+3i-4i2=15-20i+3i-4×(-1)=19-17i
(2)(5+i)(5-i)=52-i2=25-(-1)=26
解答下面问题:
(1)化简:i3=
(2)计算:(3+i)2;
(3)试一试:将
化简成a+bi的形式.
例如计算:
(1)(5+i)(3-4i)=5×3+5×(-4i)+3i-4i2=15-20i+3i-4×(-1)=19-17i
(2)(5+i)(5-i)=52-i2=25-(-1)=26
解答下面问题:
(1)化简:i3=
-i
-i
,i4=1
1
;(2)计算:(3+i)2;
(3)试一试:将
| 2+i | 2-i |
分析:(1)根据i2=-1把i3化为i2•i,把i4化为i2•i2进行计算即可;
(2)根据完全平方公式进行计算即可;
(3)根据平方差公式把原式化为
的形式进行计算即可.
(2)根据完全平方公式进行计算即可;
(3)根据平方差公式把原式化为
| (2+i)2 |
| (2-i)(2+i) |
解答:解:(1)∵i2=-1,
∴i3=i2•i=-i;i4=i2•i2=(-1)×(-1)=1;
故答案为:-i,1;
(2)原式=(3+i)2
=9+i2+6i
=9-1+6i
=8+6i;
(3)原式=
=
=
=
.
∴i3=i2•i=-i;i4=i2•i2=(-1)×(-1)=1;
故答案为:-i,1;
(2)原式=(3+i)2
=9+i2+6i
=9-1+6i
=8+6i;
(3)原式=
| (2+i)2 |
| (2-i)(2+i) |
| 4+i2+4i |
| 4-i2 |
| 4-1+4i |
| 4+1 |
| 3+4i |
| 5 |
点评:本题考查的是实数的运算,在解答此题时要注意平方差公式及完全平方公式的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
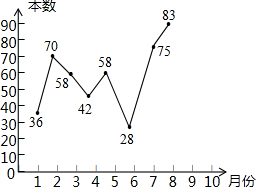 (2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
(2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )