Question

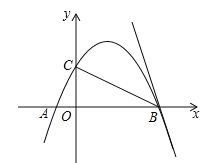
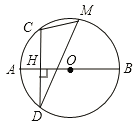
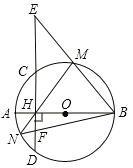
【题目】如图，线段AB 是⊙O的直径，弦CD⊥AB于点H，点M是弧CBD 上任意一点，AH=2，CH=4．

（1）求⊙O 的半径r 的长度；

（2）求sin∠CMD；

（3）直线BM交直线CD于点E，直线MH交⊙O 于点 N，连接BN交CE于点 F，求HEHF的值．

Answer 1

【答案】（1）5；（2）；（3）16

【解析】（1）在Rt△COH中，利用勾股定理即可解决问题；

（2）只要证明∠CMD=△COA，求出sin∠COA即可；

（3）由△EHM∽△NHF，推出，推出HEHF=HMHN，又HMHN=AHHB，推出HEHF=AHHB，由此即可解决问题．

（1）连接OC，

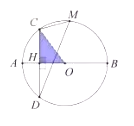
在Rt△COH中，

∵CH=4,OH=r-2,OC=r.

∴ （r-2）2+42=r2.

∴ r=5；

（2）∵弦CD与直径AB垂直，

∴，

∴ ∠AOC=∠COD，

∴∠CMD=∠COD，

∴ ∠CMD=∠AOC，

∴sin∠CMD=sin∠AOC，

在Rt△COH中，

∴sin∠AOC=，

∴sin∠CMD=；

（3）连接AM，

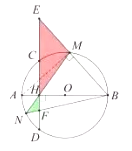
∴∠AMB=90°，

在Rt△AMB中，

∴∠MAB+∠ABM=90°，

在Rt△EHB中，

∴∠E+∠ABM=90°，

∴∠MAB=∠E，

∵ ，

∴∠MNB=∠MAB=∠E，

∵∠EHM=∠NHF，

∴△EHM∽△NHF，

∴，

∴HEHF=HMHN，

∵AB与MN交于点H，

∴HMHN=HAHB=HA（2r-HA）=2×（10-2）=16，

∴HEHF=16.