题目内容
已知α为锐角，下列结论：①sinα+cosα=1；②如果α＞45°，那么sinα＞cosα；③如果cosα＞
，那么α＜60°；④
=1-sinα，正确的有（ ）
| 1 |
| 2 |
| (sinα-1)2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析：①先画出直角三角形，然后根据三角函数的定义解答；②③④根据三角函数的增减性及特殊角的三角函数值解答．
解答：解：①如图，
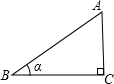
sinα=
，cosα=
，则sinα+cosα=
+
=
＞1，故结论错误；
②因为sin45°=cos45°=1，且在锐角范围内，正弦函数为增函数，余弦函数为减函数，故α＞45°时，sinα＞
，cosα＜
，于是sinα＞cosα，故结论正确；
③因为cos60°=
，且在锐角范围内，余弦函数为减函数，故cosα＞
时，α＜60°，故结论正确；
④因为在sinα≤1，所以
=1-sinα，故结论正确．
故选C．
sinα=
| AC |
| AB |
| BC |
| AB |
| AC |
| AB |
| BC |
| AB |
| AC+BC |
| AB |
②因为sin45°=cos45°=1，且在锐角范围内，正弦函数为增函数，余弦函数为减函数，故α＞45°时，sinα＞
| ||
| 2 |
| ||
| 2 |
③因为cos60°=
| 1 |
| 2 |
| 1 |
| 2 |
④因为在sinα≤1，所以
| (sinα-1)2 |
故选C．
点评：此题考查了特殊角的三角函数值及三角函数的增减性，解题时需要灵活处理，并适时利用图象．
练习册系列答案
相关题目
已知α为锐角，下列结论：
（1）sinα+cosα=1；
（2）若α＞45°，则sinα＞cosα；
（3）如果cosα＞
，则α＜60°；
（4）
=1-sinα．
其中正确结论的序号是（ ）
（1）sinα+cosα=1；
（2）若α＞45°，则sinα＞cosα；
（3）如果cosα＞
| 1 |
| 2 |
（4）
| (sinα-1)2 |
其中正确结论的序号是（ ）
| A、（1）（3）（4） |
| B、（2）（4） |
| C、（2）（3）（4） |
| D、（3）（4） |
，则α＜60°；
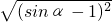=1-sinα．
，则α＜60°；
=1-sinα．
，那么α＜60°；④
=1-sinα，正确的有（ ）