题目内容
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1: 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
由上表猜想:对任意m(m>0)均有 = .请证明你的猜想.
= .请证明你的猜想.
【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为 ;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为 .

 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.【猜想与证明】
填表:
| m | 1 | 2 | 3 |
 | | | |
 = .请证明你的猜想.
= .请证明你的猜想.【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为 ;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为 .

猜想与证明:
填表为:
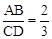 。理由见解析
。理由见解析
探究与运用:
(1) 。
。
(2)27。
联想与拓展
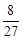 。
。
填表为:
| m | 1 | 2 | 3 |
 |  |  |  |
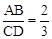 。理由见解析
。理由见解析探究与运用:
(1)
 。
。(2)27。
联想与拓展
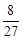 。
。试题分析:猜想与证明:
当m=1时,1=
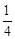 x2,1=
x2,1=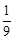 x2,∴x=±2,x=±3。∴AB=4,CD=6。∴
x2,∴x=±2,x=±3。∴AB=4,CD=6。∴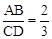 。
。当m=2时,4=
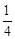 x2,4=
x2,4=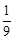 x2,∴x=±4,x=±6。∴AB=8,CD=12。∴
x2,∴x=±4,x=±6。∴AB=8,CD=12。∴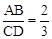 。
。当m=3时,9=
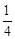 x2,9=
x2,9=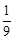 x2,∴x=±6,x=±9。∴AB=12,CD=18。∴
x2,∴x=±6,x=±9。∴AB=12,CD=18。∴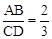 。
。探究与证明:
(1)由条件可以得出△AOB与△CQD高相等,就可以得出面积之比等于底之比而得出结论:
(2)分两种情况讨论,当△AOB为等腰直角三角形时,可以求出m的值就可以求出△AOB的面积,从而求出△CQD的面积,就可以求出其差,当△CQD为等腰直角三角形时,可以求出m的值就可以求出△CDQ的面积,进而可以求出结论。
解:猜想与证明:
填表为:
| m | 1 | 2 | 3 |
 |  |  |  |
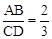 。证明如下:
。证明如下:将y=m2(m>0)代入
 ,得x=±2m,
,得x=±2m,∴A(﹣2m,m2),B(2m,m2)。∴AB=4m。
将y=m2(m>0)代入
 ,得x=±3m,
,得x=±3m,∴C(﹣3m,m2),D(3m,m2)。∴CD=6m。
∴
 。
。∴对任意m(m>0)均有
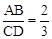 。
。探究与运用:
(1)∵O、Q关于直线CD对称,∴PQ=OP。
∵CD∥x轴,∴∠DPQ=∠DPO=90°。∴△AOB与△CQD的高相等。
∵
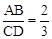 ,∴AB=
,∴AB= CD。
CD。∵S△AOB=
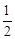 AB•PO,S△CQD=
AB•PO,S△CQD=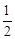 CD•PQ,∴
CD•PQ,∴ 。
。(2)当△AOB为等腰直角三角形时,如图,

∴PO=PB=m2,AB=2OP。
∴m2=
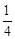 m4。∴4m2=m4,解得m1=0,m2=﹣2,m3=2。
m4。∴4m2=m4,解得m1=0,m2=﹣2,m3=2。∵m>0,∴m=2。
∴OP=4,AB=8,PD=6,CD=12。
∴S△AOB=
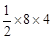 =16,S△CQD=
=16,S△CQD=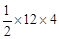 =24。
=24。∴S△CQD﹣S△AOB=24﹣16=8。
当△CQD是等腰直角三角形时,如图,

∴PQ=PO=PD=m2,CD=2QP。
∴m2=
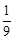 m4。∴9m2=m4,∴m1=0,m2=﹣3,m3=3。
m4。∴9m2=m4,∴m1=0,m2=﹣3,m3=3。∵m>0,∴m=3。
∴OP=6,AB=12,PQ=9,CD=18。
∴S△AOB=
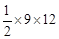 =54,S△CQD=
=54,S△CQD=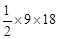 =81。
=81。∴S△CQD﹣S△AOB=81﹣54=27。
联想与拓展:
由猜想与证明可以得知A(﹣2m,m2),D(3m,m2),
∵AE∥y轴,DF∥y轴,∴E点的横坐标为﹣2m,F点的横坐标为3m。
∴y=
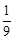 (﹣2m)2,y=
(﹣2m)2,y=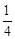 (3m)2,∴y=
(3m)2,∴y=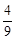 m2,y=
m2,y=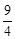 m2。∴E(﹣2m,
m2。∴E(﹣2m,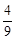 m2),F(3m,
m2),F(3m,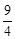 m2)。
m2)。∴AE=m2﹣
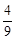 m2=
m2=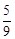 m2,DF=
m2,DF=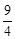 m2﹣m2=
m2﹣m2=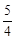 m2。
m2。∴S△AEM=
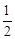 ×
×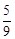 m2•2m=
m2•2m=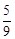 m3,S△DFM=
m3,S△DFM=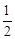 ×
×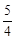 m2•3m=
m2•3m=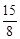 m3。∴
m3。∴ 。
。
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 中自变量x的取值范围是______________.
中自变量x的取值范围是______________. 中,自变量x的取值范围是【 】
中,自变量x的取值范围是【 】

 的自变量x的取值范围是 .
的自变量x的取值范围是 .



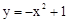
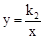 的图像没有公共点,则
的图像没有公共点,则