题目内容
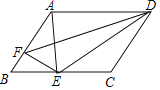
【题目】如图，点E为□ABCD的边BC上一点，线段AE的垂直平分线恰好经过点D且交AB于点F，△BEF和△CDE的周长分别为8和13，则□ABCD的周长为______________.
【答案】21
【解析】由线段垂直平分线的性质得出EF=AF，DE=AD，由三角形周长得BE+EF+BF=BE+AF+BF=BE+AB=8，CE+CD+DE=CE+CD+AD=13, 即可得出答案.
解：∵线段EC的垂直平分线恰好经过点B且交CD于点F，
∴EF=CF，BE=BC，
∵△ABE和△DEF的周长分别为13和8，
∴ABCD的周长为：AB+AD+CD+BC=（AB+AE+BC）+（DE+DF+CF）=（AB+AE+BE）+（DE+DF+EF）=13+8=21．
故答案为：21．
练习册系列答案
相关题目
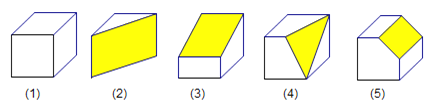
【题目】如图，图①是正方体木块，把它切去一块，得到如图②、③、④、⑤所示的木块.
(1)观察图①可以知道，正方体有8个顶点，12条棱，6个面，请你将各图中木块的顶点数、棱数、面数填入下表：
图号 | 棱数a | 顶点数b | 面数c |
① | 12 | 8 | 6 |
② | |||
③ | |||
④ | |||
⑤ |
(2)由上表各种木块的棱数、顶点数、面数之间的数量关系可以归纳出一定的规律，请你写出棱数、顶点数、面数之间的数量关系式：_______________.