题目内容
今年我国多个省市遭受严重干旱.受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8 元/千克下降至第2周的2.4 元/千克,且y与周数x的变化情况满足二次函数y=-
x2+ bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x所满足的函数关系式,并求出5月份y与x所满足的二次函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份的进价m(元/千克)与周数x所满足的函数关系为m=-
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
| 1 |
| 20 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x所满足的函数关系式,并求出5月份y与x所满足的二次函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
| 1 |
| 4 |
| 1 |
| 5 |
分析:(1)从表格看出,x每增加1,y就增加0.2,由此可确定是一次函数关系式,继而代入两点可得出4月份y与x所满足的函数关系式;再把x=1,y=2.8和x=2,y=2.4,分别代入y=-
x2+bx+c,求出b、c的值,即可确定5月份y与x所满足的二次函数关系式;
(2)设第x周销售此种蔬菜一千克时,4月份获得的利润为W1元,5月份获得的利润为W2元.先根据利润=售价-进价,分别列出W1与x,W2与x的函数解析式,再分别根据一次函数、二次函数的性质及自变量的取值范围,求解即可.
| 1 |
| 20 |
(2)设第x周销售此种蔬菜一千克时,4月份获得的利润为W1元,5月份获得的利润为W2元.先根据利润=售价-进价,分别列出W1与x,W2与x的函数解析式,再分别根据一次函数、二次函数的性质及自变量的取值范围,求解即可.
解答:解:(1)通过观察可知,四月份周数y与x符合一次函数关系,设这个关系式为:y=kx+b,
则
,
解得:
,
所以4月份y与x的函数关系式为y=0.2x+1.8;
将(1,2.8),(2,2.4)代入y=-
x2+bx+c,
可得:
,
解得:
,
所以5月份y与x的二次函数关系式为y=-
x2-
x+
;
(2)设第x周销售此种蔬菜一千克时,4月份获得的利润为W1元,5月份获得的利润为W2元.
由题意,有W1=y-m=(0.2x+1.8)-(
x+1.2),即:W1=-0.05x+0.6.
∵-0.05<0,∴W1随x的增大而减小,
又∵x为正整数,
∴当x=1时利润最大,最大值为:W=-0.05×1+0.6=0.55(元);
W2=y-m=(-
x2-
x+
)-(-
x+2),即:W2=-
x2-
x+
,
∵a=-
<0,对称轴为:x=-
=-
,
∴W2随x的增大而减小,
又∵x为正整数,
∴当x=1时利润最大,最大值为:W2=-
-
+
=1(元).
故4月份在第一周销售此种蔬菜一千克的利润最大,且最大利润是0.55元;5月份在第一周销售此种蔬菜一千克的利润最大,且最大利润是1元.
则
|
解得:
|
所以4月份y与x的函数关系式为y=0.2x+1.8;
将(1,2.8),(2,2.4)代入y=-
| 1 |
| 20 |
可得:
|
解得:
|
所以5月份y与x的二次函数关系式为y=-
| 1 |
| 20 |
| 1 |
| 4 |
| 31 |
| 10 |
(2)设第x周销售此种蔬菜一千克时,4月份获得的利润为W1元,5月份获得的利润为W2元.
由题意,有W1=y-m=(0.2x+1.8)-(
| 1 |
| 4 |
∵-0.05<0,∴W1随x的增大而减小,
又∵x为正整数,
∴当x=1时利润最大,最大值为:W=-0.05×1+0.6=0.55(元);
W2=y-m=(-
| 1 |
| 20 |
| 1 |
| 4 |
| 31 |
| 10 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 20 |
| 11 |
| 10 |
∵a=-
| 1 |
| 20 |
| b |
| 2a |
| 1 |
| 2 |
∴W2随x的增大而减小,
又∵x为正整数,
∴当x=1时利润最大,最大值为:W2=-
| 1 |
| 20 |
| 1 |
| 20 |
| 11 |
| 10 |
故4月份在第一周销售此种蔬菜一千克的利润最大,且最大利润是0.55元;5月份在第一周销售此种蔬菜一千克的利润最大,且最大利润是1元.
点评:本题考查了一次函数、二次函数解析式求法及二次函数的实际应用,解答本题的关键是求出两函数关系式,将实际问题转化为数学计算,有一定难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-
x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=-
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/kg) | 2 | 2.2 | 2.4 | 2.6 |
| 1 |
| 20 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
| 1 |
| 4 |
| 1 |
| 5 |
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
(12分)今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
【小题1】(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式;
【小题2】(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的 2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
【小题3】(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=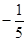 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
【小题2】(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的
 2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式【小题3】(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
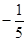 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-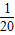 x2+bx+c.
x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m= x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=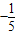 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/kg) | 2 | 2.2 | 2.4 | 2.6 |
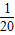 x2+bx+c.
x2+bx+c.(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
 x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=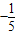 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)