题目内容
今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/kg) | 2 | 2.2 | 2.4 | 2.6 |
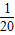 x2+bx+c.
x2+bx+c.(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
 x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=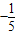 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
【答案】分析:(1)从表格看出,x每增加1,y就增加0.2,由此可确定是一次函数关系式;把x=1,y=2.8和x=2,y=2.4,分别代入y=- +bx+c可求b、c的值,确定二次函数解析式;
+bx+c可求b、c的值,确定二次函数解析式;
(2)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润;
(3)根据增长率的公式,列出方程求解即可.
解答:解:(1)4月份y与x满足的函数关系式为y=0.2x+1.8
把x=1,y=2.8和x=2,y=2.4,分别代入y=- +bx+c得
+bx+c得

解得: ,
,
∴5月份y与x满足的函数关系式为y=-0.05x2-0.25x+3.1;
(2)设4月份第x周销售此种蔬菜一千克的利润为W1元,5月份第x周销售此种蔬菜一千克的利润为W2元.则:
W1=(0.2x+1.8)-( x+1.2)=-0.05x+0.6
x+1.2)=-0.05x+0.6
∵-0.05<0,∴W1随x的增大而减少
∴当x=1时,W1最大=-0.05+0.6=0.55
W2=(-0.05x2-0.25x+3.1)-(- x+2)=-0.05x2-0.05x+1.1
x+2)=-0.05x2-0.05x+1.1
∵对称轴为x=- =-0.5,且-0.05<0,
=-0.5,且-0.05<0,
∴当x=1时,W2最大=1
∴4月份销售此种蔬菜一千克的利润在第1周最大,最大利润为0.55元,
5月份销售此种蔬菜一千克的利润在第1周最大,最大利润为1元.
(3)由题意知:[100(1-a%)+2]×2.4(1+0.8a%)=2.4×100,
整理,得a2+23a-250=0,解得a=
∵392=1521,402=1600,而1529更接近1521,∴取 ≈39
≈39
∴a≈-31(舍去)或a≈8.
点评:本题考查了一次函数、二次函数解析式求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
 +bx+c可求b、c的值,确定二次函数解析式;
+bx+c可求b、c的值,确定二次函数解析式;(2)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润;
(3)根据增长率的公式,列出方程求解即可.
解答:解:(1)4月份y与x满足的函数关系式为y=0.2x+1.8
把x=1,y=2.8和x=2,y=2.4,分别代入y=-
 +bx+c得
+bx+c得
解得:
 ,
,∴5月份y与x满足的函数关系式为y=-0.05x2-0.25x+3.1;
(2)设4月份第x周销售此种蔬菜一千克的利润为W1元,5月份第x周销售此种蔬菜一千克的利润为W2元.则:
W1=(0.2x+1.8)-(
 x+1.2)=-0.05x+0.6
x+1.2)=-0.05x+0.6∵-0.05<0,∴W1随x的增大而减少
∴当x=1时,W1最大=-0.05+0.6=0.55
W2=(-0.05x2-0.25x+3.1)-(-
 x+2)=-0.05x2-0.05x+1.1
x+2)=-0.05x2-0.05x+1.1∵对称轴为x=-
 =-0.5,且-0.05<0,
=-0.5,且-0.05<0,∴当x=1时,W2最大=1
∴4月份销售此种蔬菜一千克的利润在第1周最大,最大利润为0.55元,
5月份销售此种蔬菜一千克的利润在第1周最大,最大利润为1元.
(3)由题意知:[100(1-a%)+2]×2.4(1+0.8a%)=2.4×100,
整理,得a2+23a-250=0,解得a=

∵392=1521,402=1600,而1529更接近1521,∴取
 ≈39
≈39∴a≈-31(舍去)或a≈8.
点评:本题考查了一次函数、二次函数解析式求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=-
x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=-
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/kg) | 2 | 2.2 | 2.4 | 2.6 |
| 1 |
| 20 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式,并求出5月份y与x的函数关系式;
(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
| 1 |
| 4 |
| 1 |
| 5 |
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a%,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8a%.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
(12分)今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
【小题1】(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式;
【小题2】(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的 2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
【小题3】(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=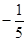 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
【小题2】(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的
 2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式
2.4元/千克,且y与周数x的变化情况满足二次函数y=- x2+bx+c. ,请求出5月份y与x的函数关系式【小题3】(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
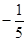 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?