题目内容
【题目】如图，在正方形ABCD中，E是AD上一点，F是BA延长线上的一点，AF=AE，．
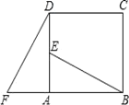
（1）求证：△ABE≌△ADF
（2）线段BE与DF有什么关系？证明你的结论．
【答案】（1）见解析；（2）(2)BE=DF，BE⊥DF；证明见解析
【解析】
（1）根据正方形的性质和SAS即可证明；
（2）根据旋转的性质得出△ABE≌△ADF，从而得出BE=DF，再根据正方形的性质得出BE⊥DF．
(1)∵ ABCD是正方形，
∴DA=BA,∠DAB=∠DAF=90°，
在△ABE和△ADF中，
,
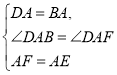∴△ABE≌△ADF（SAS）
证明：(2)BE=DF，BE⊥DF；
延长BE交DF于G；
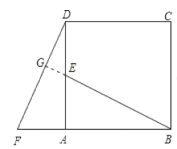
由△ABE≌△ADF，得BE=DF，∠ABE=∠ADF；
又∠AEB=∠DEG；
∴∠DGB=∠DAB=90°；
练习册系列答案
相关题目
